리만제타함수 계산
리만제타함수 양자역학
리만제타함수 해석적확장
리만 제타 함수 영점
리만 제타 함수 자명한 근
리만 제타 함수 소수
리만 제타 함수 그래프
리만 가설이 중요한 이유
주제에 대한 기사를 찾고 있습니까 “리만 제타 함수“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: 292 사진을 다운로드할 수 있는 최고의 웹사이트. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.
이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.
컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.
는 소수들의 정수론적 성질을 해석적으로 내포하는 유리형 함수이다. 해석적 수론에서 소수의 분포를 연구할 때 핵심적인 역할을 하며, 또한 L-함수 이론의 모태이다.
Table of Contents
리만 제타 함수 주제와 관련된 상위 29 이미지
주제 리만 제타 함수 와 관련된 16 개의 이미지가 있습니다.
- Image source: twitter.com
- Views: 73680
- Publish date: 14 minute ago
- Downloads: 45057
- Likes: 4197
- Dislikes: 8
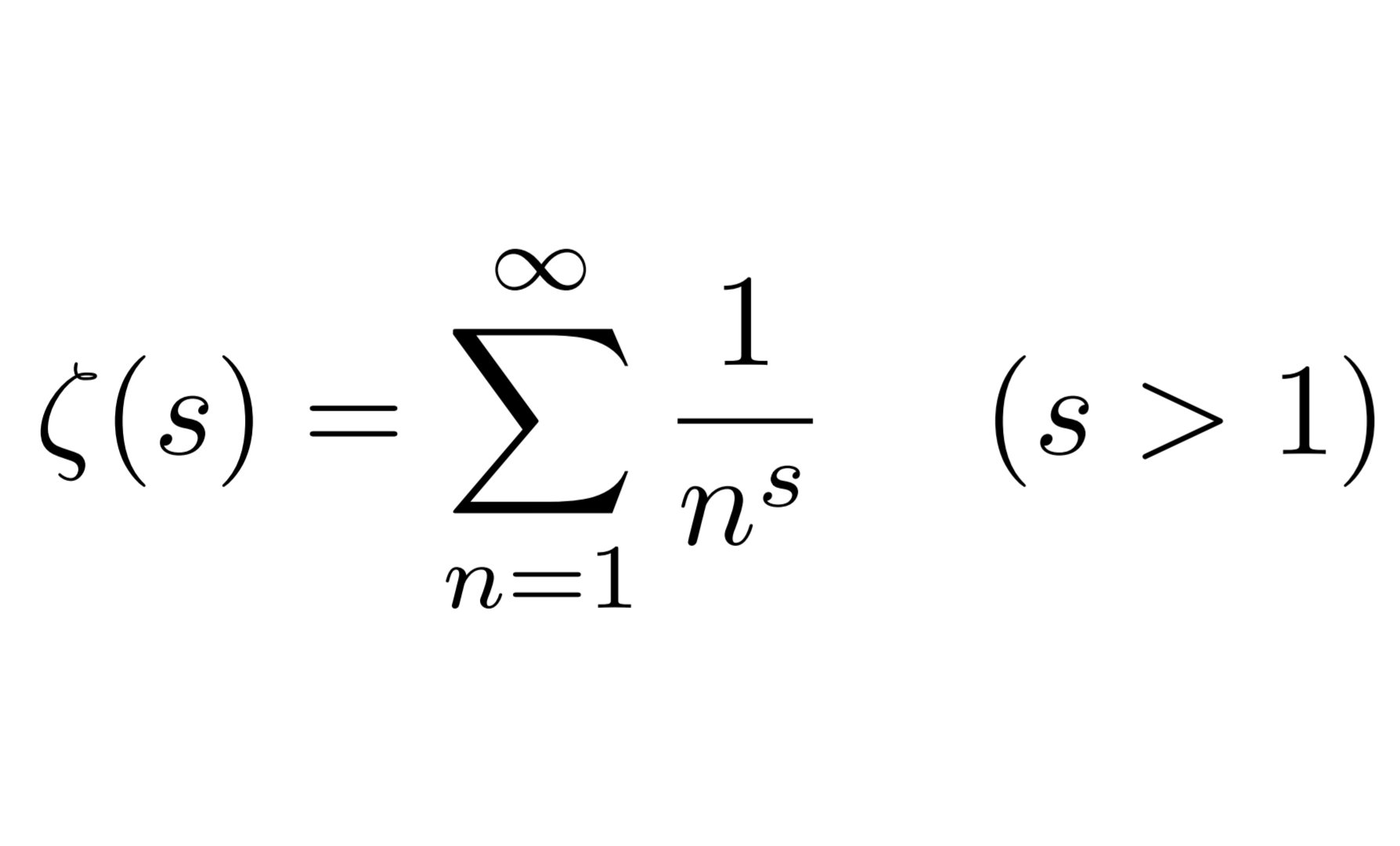
Something went wrong, but don’t fret — let’s give it another shot.
Seminar #2 소수와 리만 제타 함수 – POSTECH Undergraduate Math Seminar
연사: 수학과 김창영일시: 2019.03.22 (금)Lunch 12:00~13:00, Lecture 13:00~14:00 유일한 세계 7대 밀레니엄 문제이자 힐베르트 23가지 문제에 포함되어 있는 리만 가설. 그 리만 가설에 대해 학부 수준에서 이해해보려 한다. 리만 제타 함수의 신비한 성질들과 감마 함수와의 관계, 마지막으로 소수 세기 함수와의 관계…
- Image source: postechmathseminar.wordpress.com
- Views: 109071
- Publish date: 44 minute ago
- Downloads: 73436
- Likes: 5514
- Dislikes: 2

유일한 세계 7대 밀레니엄 문제이자 힐베르트 23가지 문제에 포함되어 있는 리만 가설. 그 리만 가설에 대해 학부 수준에서 이해해보려 한다. 리만 제타 함수의 신비한 성질들과 감마 함수와의 관계, 마지막으로 소수 세기 함수와의 관계를 알아보려고 한다. 리만 가설과 소수의 비밀 사이의 관계를 알아본 후 발표자가 생각해본 여러 제타 함수의 성질과 쌍둥이 소수의 부분적 풀이법을 말해보려 한다.
개인정보 및 쿠키: 이 사이트에서는 쿠키를 사용합니다. 이 웹사이트를 계속 사용하면 해당 사용에 동의하는 것입니다.
아래 항목을 채우거나 오른쪽 아이콘 중 하나를 클릭하여 로그 인 하세요:
L-함수 – 위키백과, 우리 모두의 백과사전
- Image source: ko.wikipedia.org
- Views: 52963
- Publish date: 31 minute ago
- Downloads: 15169
- Likes: 8228
- Dislikes: 8
O. Shanker (2006). “Random matrices, generalized zeta functions and self-similarity of zero distributions”. 《J. Phys. A: Math. Gen.》
가 해석적 관점에서 정확한 L-함수를 제공하는 방법으로 구축된다는 것이 명확해졌다. 즉 자기동형 사상과 관련되는 방식이어야 한다는 것이다. 일반적으로는 다수의 다른 연구 프로그램을 개념 수준에서 통합한다.
을 만든다. 이 오일러 곱이 복소 상반평면의 오른쪽 일부에서 수렴하는 것을 증명할 수 있는지 확인한다. 그리고 복소 평면의 나머지 영역에서도 해석적 확장을 통해 정의될 수 있는지 확인한다 (몇몇
제타함수 증명 : 네이버 블로그
리만제타함수보다 오일러제타함수가 더 중요하다 제타함수의 기본은 오일러제타함수이고 산수 지식만 가지…
- Image source: m.blog.naver.com
- Views: 39623
- Publish date: 7 hours ago
- Downloads: 102584
- Likes: 6359
- Dislikes: 6
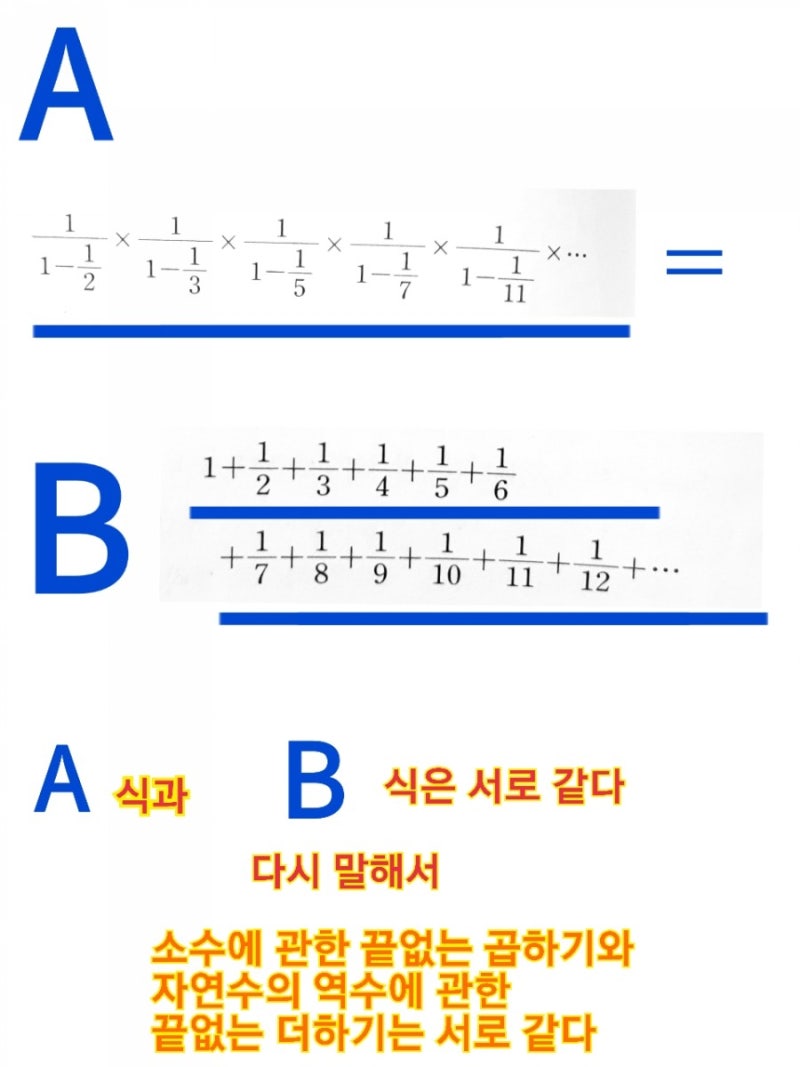
알기 쉽게 간결하게 설명하는 게 최고다
산수 지식만 가지고도 이해할 수 있다
- Image source: namu.wiki
- Views: 34624
- Publish date: 27 minute ago
- Downloads: 109021
- Likes: 8135
- Dislikes: 7
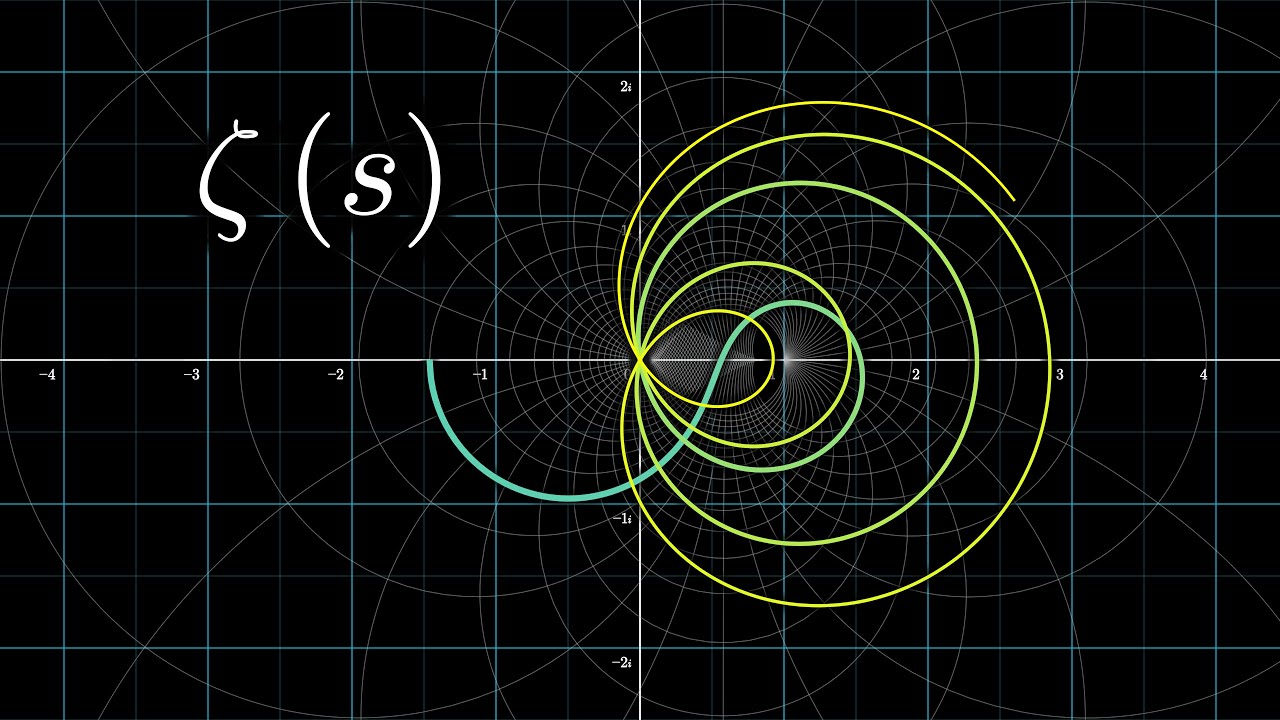
리만 가설이 양자 역학과 유사점이 있다네요. : 클리앙
수포자라 뭔 소린지 몰라서 이리저리 찾아봤는데 1972년 수학자인 휴 로웰 몽고메리 과 물리학자인 프리먼 다이슨이 우연찮은 짧은 만남을 가지게 되는데 그 짧은 만남중에 리만 가설과 양자역학의 유사점에 처음으로 발견 되었다네요. 이상 수포자라 더 이상의 설명은… 몰라유. ㅎㅎ;;
- Image source: www.clien.net
- Views: 78106
- Publish date: 4 minute ago
- Downloads: 1195
- Likes: 7604
- Dislikes: 8

1972년 수학자인 휴 로웰 몽고메리 과 물리학자인 프리먼 다이슨이 우연찮은 짧은 만남을 가지게 되는데 그 짧은 만남중에 리만 가설과 양자역학의 유사점에 처음으로 발견 되었다네요.
https://www.americanscientist.org/article/the-spectrum-of-riemannium
2022-03-04 09:49:43 / 수정일: 2022-03-04 09:53:39
- Image source: namu.wiki
- Views: 47593
- Publish date: 22 hours ago
- Downloads: 73356
- Likes: 954
- Dislikes: 6

Riemann zeta function values at z=0, 1, 2, -1, -2 계산
심심해서 리만 제타함수의 zeta(-1) 을 계산해 보다, 아주 중요한 계산중 하나이다.
- Image source: m.blog.daum.net
- Views: 4660
- Publish date: 13 hours ago
- Downloads: 49570
- Likes: 5108
- Dislikes: 1

2007 JGK xi(1)=0 , xi(0)=-1 or -00 vs 1859 Riemann xi(1)=xi(0)=1/2
리만가설 증명/ 김정건 ( Proof of Riemann Hypothesis by JG Kim, 2007 )
리만가설 증명/ 김정건 ( Proof of Riemann Hypothesis by JG Kim, 2007 )
Curiosa mathematica 수학 실수 부 리만 제타 함수 포인트, 수학, 각도, 본문 png | PNGEgg
- Image source: www.pngegg.com
- Views: 93957
- Publish date: 42 minute ago
- Downloads: 8497
- Likes: 8997
- Dislikes: 7

Curiosa mathematica 수학 실수 부 리만 제타 함수 포인트, 수학, 각도, 본문 png
png 다운로드 ( 270.62KB )
비상업적 용도, DMCA
딥러닝과 소수
과학을 잘 모르지만 과학을 좋아하고, 수포자이지만 수학을 좋아하는 제가 최근에 저를 사로잡은 내용이 있었습니다. 이름하여 바로 ‘리만 가설’ 입니다. 리만 가설 (Riemann hypothesis) 개발자 블로그에 무슨 뚱딴지 같은 이야기라구요? 수학을 잘 모르지만 개발자가 된 이상 간단한 4칙연산 뿐만 아니라 점점 더 어려운 고등수학을 살짝 발 담을 일이 많아집니다. (잘 모르셨겠지만요) 일단 리만 가설이라는 것을 알아봅시다. 리만 제타 추측은 리만 제타 함수의 모든 자명하지 않은 영점의 실수부가 1/2 이라는 추측이다. 아니 이게 무슨 말일까요… 소수 (prime…
- Image source: bravenamme.github.io
- Views: 58637
- Publish date: 24 minute ago
- Downloads: 106649
- Likes: 1270
- Dislikes: 4

하지만 ‘오일러의 공식’으로 유명한 수학자 레온하르트 오일러(1707~1783)는 소수를 관찰하면서 소수로만 이뤄진 식을 하나 만들었다. 소수의 제곱을 소수의 제곱에서 1을 뺀 수로 나눈 뒤 끊임없이 곱하는 식(1번 식)을 정리했더니 ‘파이(원주율)’가 나타났다.
리만은 오일러의 함수를 변형하여 입체적인 그래프를 만드는데, 놀랍게도 이 그래프에서 리만이 계산한 4개의 비자명 근이 복소평면 위에서 모두 일직선상에 있었습니다.
그냥 무시하고 머신러닝 알고리즘을 훈련 시키려고 해도 입력한 데이터에 가까운 무언가만 가지게 될 것이며. 실제 예측이랑 터무니 없는 답만 나올 것이기 때문입니다.
Riemann zeta function values at z=0, 1, 2, -1, -2 계산
심심해서 리만 제타함수의 zeta(-1) 을 계산해 보다, 아주 중요한 계산중 하나이다.
- Image source: m.blog.daum.net
- Views: 18325
- Publish date: 14 hours ago
- Downloads: 23456
- Likes: 671
- Dislikes: 1

2007 JGK xi(1)=0 , xi(0)=-1 or -00 vs 1859 Riemann xi(1)=xi(0)=1/2
리만가설 증명/ 김정건 ( Proof of Riemann Hypothesis by JG Kim, 2007 )
리만가설 증명/ 김정건 ( Proof of Riemann Hypothesis by JG Kim, 2007 )
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | YES24 블로그
선생님이 1부터 100까지 더하는 문제를 냈는데 어린 가우스는 단번에 답을 말했다고 한다. 답은 바로 101*100/2=5050이다. 1부터 100까지 숫자를 한 줄로 늘어트려 놓았을 때, 차례대로 양끝의 숫자 두 개를 더하면 항상 101이다(1…
- Image source: blog.yes24.com
- Views: 100253
- Publish date: 3 minute ago
- Downloads: 97919
- Likes: 336
- Dislikes: 5
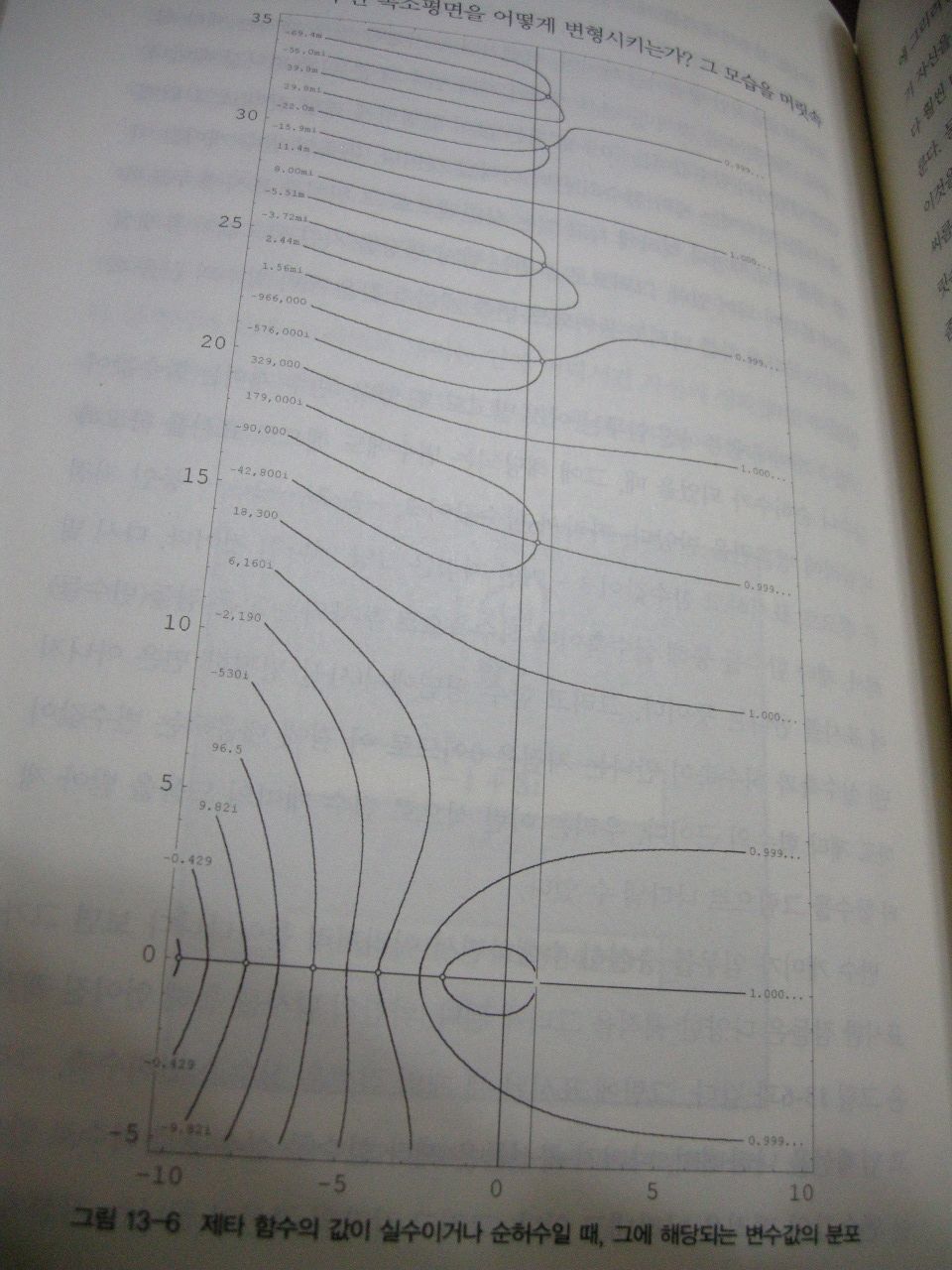
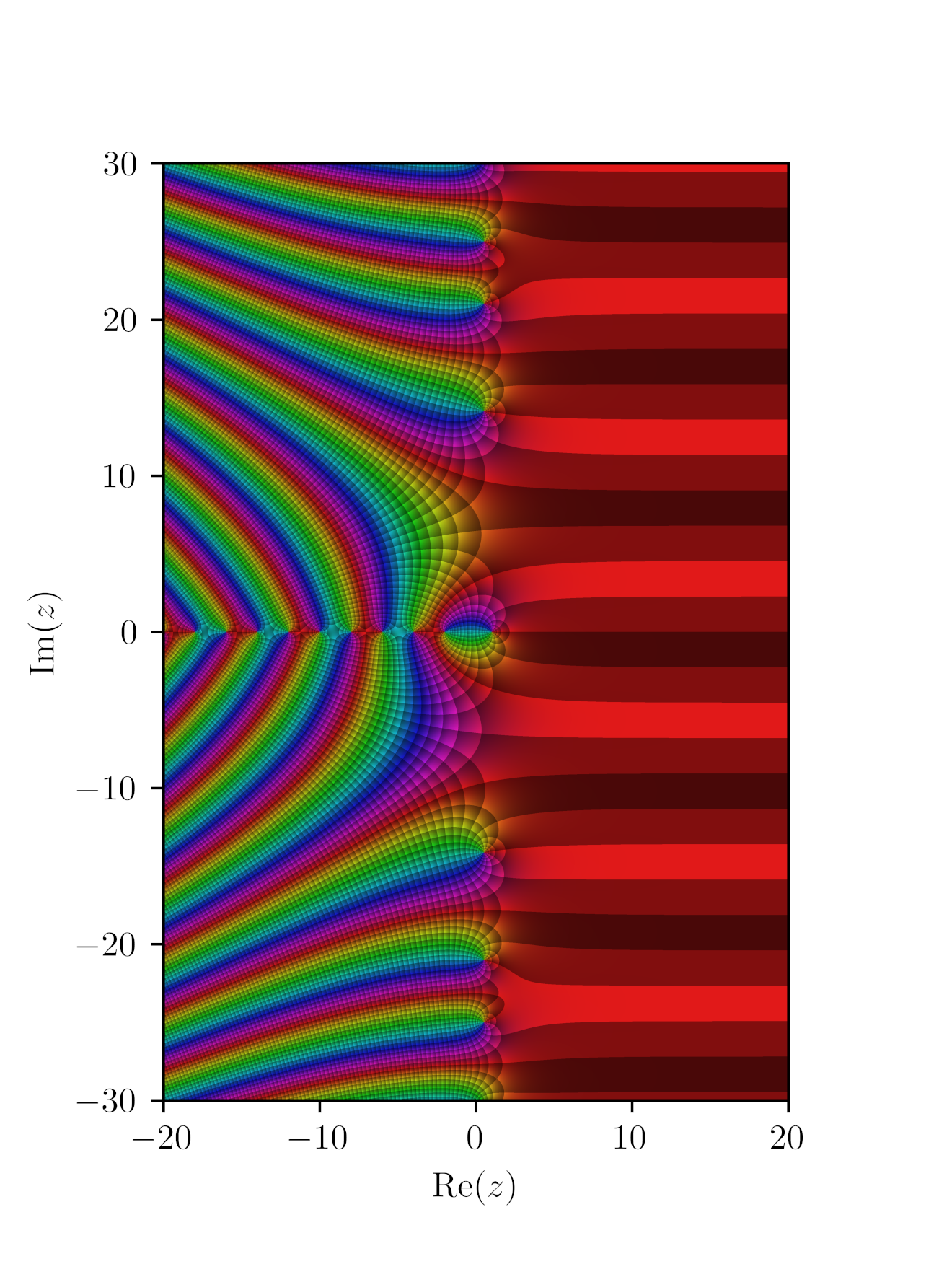
)을 이해하기 위해서는 소수정리를 비롯하여 조화수열, 로그함수, 미적분, 확률, 제타 함수, 복소평면 등의 수학지식을 알고 있어야 한다(알고 있어도 제대로 이해하는 사람은 드물다고 한다). 즉, 진입장벽이 높다. 제타 함수 하나만 해도 정말 특이하고 이해하기 어려운 함수이다. 이 제타 함수를 복소평면에 나타내고 자명하지 않는(허수인) 근들의 실수부가 1/2인 것을 구하는 것만 해도 많은 시간이 걸릴 것이다. 그렇기 때문에 수학에 관심이 있는 사람들만 리만 가설에 도전한다. 이렇게 난해한 리만 가설을 일반인들이 알기 쉽게 책으로 펴냈다는 것은 정말 대단한 것이다. 수학에 대한 전문적인 지식이 없는 일반인들은 이 책 한 권으로 리만 가설을 이해할 수 있다고 나는 말할 수 있다! 저자 더비셔는 리만 가설의 그 높은 진입장벽은 걸어서 넘을 정도로 낮춰줬다. 저자는 아직도 풀리지 않고 있는 리만 가설을 대중들에게 설명하고 혹시나 그 대중들이 관심을 가져서 리만 가설이 풀어지기를 기대한 것은 아닐까?
그 밖에 오일러(러시아의 표트르 대제에게 스카웃당한) 등의 수학자들과 관련된 흥미로운 이야기가 등장한다. 이 책의 짝수장을 들여다보면 수학의 역사와 전통적인 분류(산술학, 기하학, 대수학, 해석학)에 대하여 알 수 있다. 저자는 짝수장에 이런 이야기를 배치함으로써 독자들이 지치지 않도록 배려한 것 같다. 로그 적분 함수 Li(N)는 소수 계량 함수 π(N)(N보다 작은 소수의 개수)에 근접한다. 리만 가설을 증명하면 소수 계량 함수를 정확히 파악할 수 있다. 하지만 지금까지 전 세계의 수학자들은 못 풀고 있다. 물론, 수학에서 풀리지 않는 문제들은 많다. 리만 가설은 언제 풀릴지 아무도 장담할 수 없다고 한다. 저자가 일반인을 위해 리만 가설을 설명한 책을 낸 것은 소수 계량 함수 π(N)에 근접하려는 로그 적분 함수 Li(N)라는 생각이 든다.
그래서 300여개의 작은 독일 국가들이 34개의 독립국(오스트리아와 프러시아 포함)과 4개의 자유도시로 통합되었는데 리만은 그 중에 하나인 하노버 왕국의 동쪽인 브레젤렌츠에서 태어났다고 한다. 훔볼트의 개혁으로 수학에서 변방이었던 독일은 두각을 나타낸다. 베를린학술원이 생겼고 리만은 그 혜택을 받은 것 같다. 리만은 괴팅겐대학에 오랫동안 머물면서 연구한다. 괴팅겐대학에는 유명한 수학자인 가우스와 디리클레가 있었다. 리만은 두 수학자를 존경했고 디리클레의 제자였다. 가우스와 디리클레(오일러가 발견한 황금열쇠를 찾아낸)와 리만으로 이어지는 과정에서 리만 가설이 나온 것이다. 리만은 1859년(33세)에 베를린학술원의 회원이 되어 한 편의 논문(주어진 수보다 작은 소수의 개수에 대한 연구)을 냈고 그 논문은 수학의 역사를 바꿔놓았다.
Redirect
- Image source: www.ibric.org
- Views: 69408
- Publish date: 26 minute ago
- Downloads: 56102
- Likes: 8279
- Dislikes: 4
![수학] 새로운 오일러 스타일 공식 > Bric” style=”width:100%”><figcaption>수학] 새로운 오일러 스타일 공식 > Bric</figcaption></figure>
</div>
<hr>
<p>제타 함수란?</p>
<p><p>제타함수를 처음 연구한 수학자는 오일러(Euler)다. 그 연구를 이어 받아 정의역을 복소수 영역까지 확장하고, 소수(Prime Number)의 연구까지 진행한 인물이 바로 리만(Riemann) 이다. 최고의 수학자들이 무슨 생각을 했는지 한번 알아보자. #제타 함수의 정의 제타함수의 정의는 간단하다. 고등학교에서 배운 무한급수를 다시 보는 것 같다. s에 따라 값이 달라진다. s가 1보다 크거나 값으면 수렴할 것 같은데, 값을 계산하기가 쉽지는 않다. 그래도 계산을 해보자. 아래의 그래프는 s=1일 때의 제타함수(파란색)과 1/x를 1부터 10까지(빨간색) 그린 것이다. 다음의 수식이 성립함을 직관적으로 알 수 있다. 제타함수에서 k = 1 ~ N까지의 부분합과 적분과의 관계이다. 다항식의 적분은 쉽게..</p>
</p>
<ul>
<li><span>Image source: dowhati1.tistory.com</span></li>
<li><span>Views: 92218</span></li>
<li><span>Publish date: 20 minute ago</span></li>
<li><span>Downloads: 58237</span></li>
<li><span>Likes: 1496</span></li>
<li><span>Dislikes: 7</span></li>
</ul>
<div>
<figure><img decoding=](https://www.ibric.org/upload/geditor/201407/0.03676800_1405035258.png)
지금까지는 제타함수는 s > 1인 실수 구간에서만 정의가 되었다. 해석적 확장(Analytic Continuation)이라고 불리는 작업을 통해 s = 1 아닌 모든 복소수에 대해서 정의되는 함수로 확장해 보자.
위의 수식(오일러 곱셈 공식, Euler Product Formula)으로 부터 제타함수를 제대로 파악할 수 있으면 소수의 규칙도 알 수 있을 것 같다.
x가 0에 가까이 갈때 sin(x) = x이기 때문에, 극한의 상황을 만족하기 위해서 위 수식을 아래와 같이 변경해 볼 수 있다.
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | YES24 블로그 – 내 삶의 쉼표
선생님이 1부터 100까지 더하는 문제를 냈는데 어린 가우스는 단번에 답을 말했다고 한다….
- Image source: m.blog.yes24.com
- Views: 10281
- Publish date: 24 hours ago
- Downloads: 80213
- Likes: 1131
- Dislikes: 10

)을 이해하기 위해서는 소수정리를 비롯하여 조화수열, 로그함수, 미적분, 확률, 제타 함수, 복소평면 등의 수학지식을 알고 있어야 한다(알고 있어도 제대로 이해하는 사람은 드물다고 한다). 즉, 진입장벽이 높다. 제타 함수 하나만 해도 정말 특이하고 이해하기 어려운 함수이다. 이 제타 함수를 복소평면에 나타내고 자명하지 않는(허수인) 근들의 실수부가 1/2인 것을 구하는 것만 해도 많은 시간이 걸릴 것이다. 그렇기 때문에 수학에 관심이 있는 사람들만 리만 가설에 도전한다. 이렇게 난해한 리만 가설을 일반인들이 알기 쉽게 책으로 펴냈다는 것은 정말 대단한 것이다. 수학에 대한 전문적인 지식이 없는 일반인들은 이 책 한 권으로 리만 가설을 이해할 수 있다고 나는 말할 수 있다! 저자 더비셔는 리만 가설의 그 높은 진입장벽은 걸어서 넘을 정도로 낮춰줬다. 저자는 아직도 풀리지 않고 있는 리만 가설을 대중들에게 설명하고 혹시나 그 대중들이 관심을 가져서 리만 가설이 풀어지기를 기대한 것은 아닐까?
그 밖에 오일러(러시아의 표트르 대제에게 스카웃당한) 등의 수학자들과 관련된 흥미로운 이야기가 등장한다. 이 책의 짝수장을 들여다보면 수학의 역사와 전통적인 분류(산술학, 기하학, 대수학, 해석학)에 대하여 알 수 있다. 저자는 짝수장에 이런 이야기를 배치함으로써 독자들이 지치지 않도록 배려한 것 같다. 로그 적분 함수 Li(N)는 소수 계량 함수 π(N)(N보다 작은 소수의 개수)에 근접한다. 리만 가설을 증명하면 소수 계량 함수를 정확히 파악할 수 있다. 하지만 지금까지 전 세계의 수학자들은 못 풀고 있다. 물론, 수학에서 풀리지 않는 문제들은 많다. 리만 가설은 언제 풀릴지 아무도 장담할 수 없다고 한다. 저자가 일반인을 위해 리만 가설을 설명한 책을 낸 것은 소수 계량 함수 π(N)에 근접하려는 로그 적분 함수 Li(N)라는 생각이 든다.
그래서 300여개의 작은 독일 국가들이 34개의 독립국(오스트리아와 프러시아 포함)과 4개의 자유도시로 통합되었는데 리만은 그 중에 하나인 하노버 왕국의 동쪽인 브레젤렌츠에서 태어났다고 한다. 훔볼트의 개혁으로 수학에서 변방이었던 독일은 두각을 나타낸다. 베를린학술원이 생겼고 리만은 그 혜택을 받은 것 같다. 리만은 괴팅겐대학에 오랫동안 머물면서 연구한다. 괴팅겐대학에는 유명한 수학자인 가우스와 디리클레가 있었다. 리만은 두 수학자를 존경했고 디리클레의 제자였다. 가우스와 디리클레(오일러가 발견한 황금열쇠를 찾아낸)와 리만으로 이어지는 과정에서 리만 가설이 나온 것이다. 리만은 1859년(33세)에 베를린학술원의 회원이 되어 한 편의 논문(주어진 수보다 작은 소수의 개수에 대한 연구)을 냈고 그 논문은 수학의 역사를 바꿔놓았다.
비디오 리만 제타 함수 전설의 시작 | 바젤 문제 그리고 리만 제타 함수
- Source: Youtube
- Views: 63240
- Date: 27 minute ago
- Download: 722
- Likes: 5850
- Dislikes: 1
주제에 대한 관련 정보 리만 제타 함수
Bing에서 리만 제타 함수 주제에 대한 최신 정보를 볼 수 있습니다.
리만제타함수 계산
리만제타함수 양자역학
리만제타함수 해석적확장
리만 제타 함수 영점
리만 제타 함수 자명한 근
리만 제타 함수 소수
리만 제타 함수 그래프
리만 가설이 중요한 이유
주제에 대한 기사 보기를 마쳤습니다 리만 제타 함수. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.
리만제타함수 계산
리만제타함수 양자역학
리만제타함수 해석적확장
리만 제타 함수 영점
리만 제타 함수 자명한 근
리만 제타 함수 소수
리만 제타 함수 그래프
리만 가설이 중요한 이유