베스트 1184 로지스틱 회귀분석 해석 업데이트 43 일 전

by

로지스틱 회귀분석 해석 in r

python 로지스틱 회귀분석 해석

다항 로지스틱 회귀분석 해석

spss 로지스틱 회귀분석 해석

로지스틱 회귀분석 예제

로지스틱 회귀분석 오즈비 해석

stata 로지스틱 회귀분석 해석

로지스틱 회귀분석 논문 표

주제에 대한 기사를 찾고 있습니까 “로지스틱 회귀분석 해석“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: 974 사진을 다운로드할 수 있는 최고의 웹사이트. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.

이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.

컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.

로지스틱 회귀분석 해석 주제와 관련된 상위 131 이미지

주제 로지스틱 회귀분석 해석 와 관련된 33 개의 이미지가 있습니다.

로지스틱 회귀분석 | DataLatte’s IT Blog

로지스틱 회귀분석 로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다. 로지스틱 회귀분석 모형에서는 종속변수가 이항분포를 따르고 그 모수 $ \theta $ 가 독립변수 $ x $ 에 의존한다고 가정한다. p(y \mid x) = \text{Bin} (y; \theta (x), N) 위 식에

  • Image source: heung-bae-lee.github.io
  • Views: 71137
  • Publish date: 9 minute ago
  • Downloads: 68700
  • Likes: 4943
  • Dislikes: 8
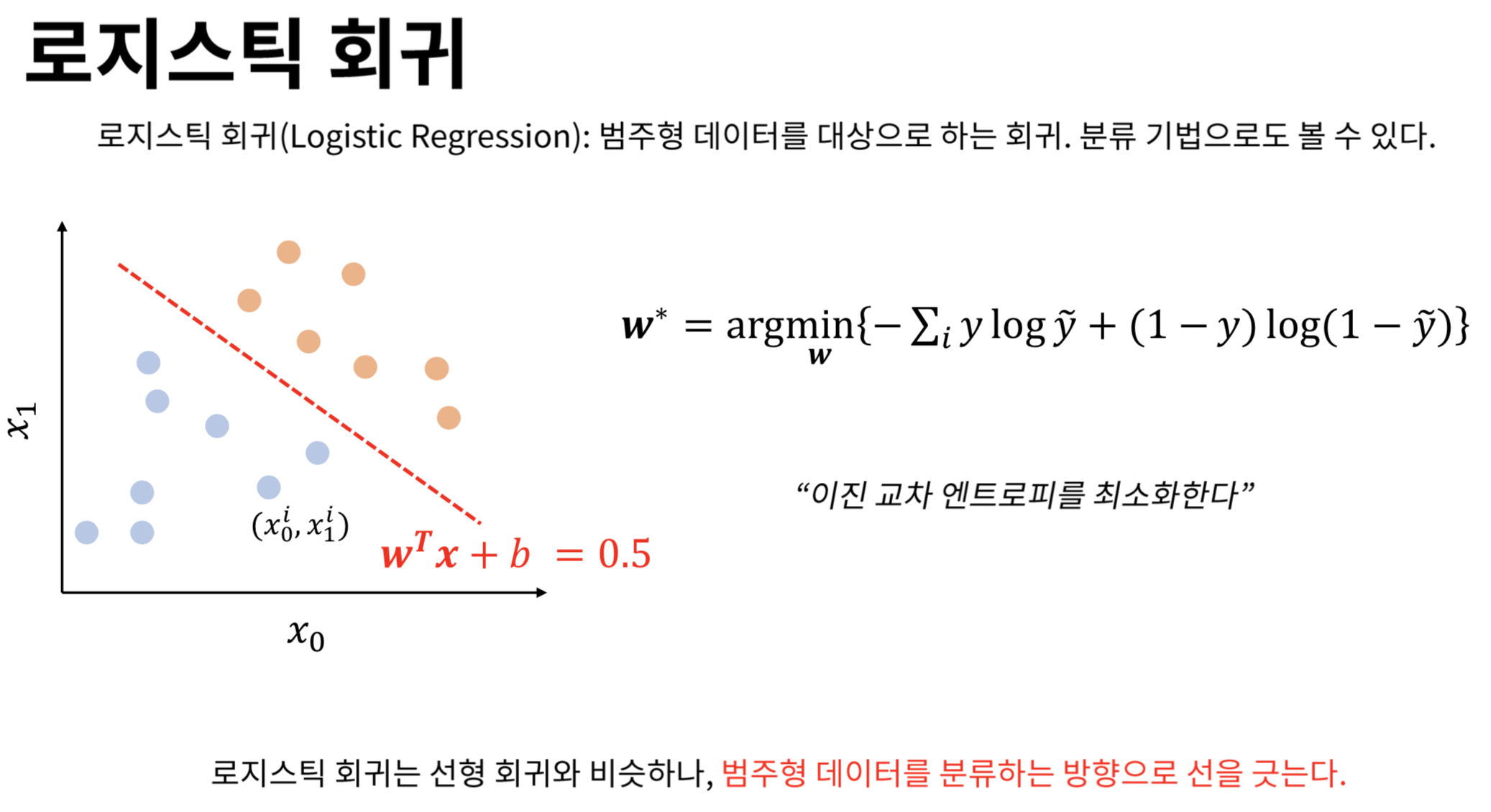
로지스틱 회귀분석 | Datalatte'S It Blog
로지스틱 회귀분석 | Datalatte’S It Blog

그레디언트 벡터가 영벡터가 되는 모수의 값이 로그가능도를 최대화하는 값이다. 하지만 그레디언트 벡터 수식이 $ w $ 에 대한 비선형 함수이므로 선형모형과 같이 간단하게 그레디언트가 0이 되는 모수 $ w $ 값에 대한 수식을 구할 수 없으며 수치적인 최적화 방법(numerical optimization)을 통해 반복적으로 최적 모수 $ w $ 의 값을 구해야 한다.

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

0부터 1사이의 값만 가지는 확률값인 $ \theta (x) $ 를 오즈비로 변환하면 0부터 양의 무한대까지의 값을 가질 수 있다. 오즈비를 로그변환한 것이 위에서 언급한 Logit function이다. 이로써 로지트 함수의 값은 로그변환에 의해 음의 무한대 $(- \infty)$부터 양의 무한대$(\infty)$까지의 값을 가질 수 있다.

로지스틱 회귀분석 | DataLatte’s IT Blog

로지스틱 회귀분석 로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다. 로지스틱 회귀분석 모형에서는 종속변수가 이항분포를 따르고 그 모수 $ \theta $ 가 독립변수 $ x $ 에 의존한다고 가정한다. p(y \mid x) = \text{Bin} (y; \theta (x), N) 위 식에

  • Image source: heung-bae-lee.github.io
  • Views: 83148
  • Publish date: 28 minute ago
  • Downloads: 89502
  • Likes: 3509
  • Dislikes: 9
로지스틱 회귀분석 | Datalatte'S It Blog
로지스틱 회귀분석 | Datalatte’S It Blog

그레디언트 벡터가 영벡터가 되는 모수의 값이 로그가능도를 최대화하는 값이다. 하지만 그레디언트 벡터 수식이 $ w $ 에 대한 비선형 함수이므로 선형모형과 같이 간단하게 그레디언트가 0이 되는 모수 $ w $ 값에 대한 수식을 구할 수 없으며 수치적인 최적화 방법(numerical optimization)을 통해 반복적으로 최적 모수 $ w $ 의 값을 구해야 한다.

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

0부터 1사이의 값만 가지는 확률값인 $ \theta (x) $ 를 오즈비로 변환하면 0부터 양의 무한대까지의 값을 가질 수 있다. 오즈비를 로그변환한 것이 위에서 언급한 Logit function이다. 이로써 로지트 함수의 값은 로그변환에 의해 음의 무한대 $(- \infty)$부터 양의 무한대$(\infty)$까지의 값을 가질 수 있다.

로지스틱 회귀분석 | DataLatte’s IT Blog

로지스틱 회귀분석 로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다. 로지스틱 회귀분석 모형에서는 종속변수가 이항분포를 따르고 그 모수 $ \theta $ 가 독립변수 $ x $ 에 의존한다고 가정한다. p(y \mid x) = \text{Bin} (y; \theta (x), N) 위 식에

  • Image source: heung-bae-lee.github.io
  • Views: 101902
  • Publish date: 53 minute ago
  • Downloads: 25555
  • Likes: 2330
  • Dislikes: 9
로지스틱 회귀분석 | Datalatte'S It Blog
로지스틱 회귀분석 | Datalatte’S It Blog

그레디언트 벡터가 영벡터가 되는 모수의 값이 로그가능도를 최대화하는 값이다. 하지만 그레디언트 벡터 수식이 $ w $ 에 대한 비선형 함수이므로 선형모형과 같이 간단하게 그레디언트가 0이 되는 모수 $ w $ 값에 대한 수식을 구할 수 없으며 수치적인 최적화 방법(numerical optimization)을 통해 반복적으로 최적 모수 $ w $ 의 값을 구해야 한다.

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

0부터 1사이의 값만 가지는 확률값인 $ \theta (x) $ 를 오즈비로 변환하면 0부터 양의 무한대까지의 값을 가질 수 있다. 오즈비를 로그변환한 것이 위에서 언급한 Logit function이다. 이로써 로지트 함수의 값은 로그변환에 의해 음의 무한대 $(- \infty)$부터 양의 무한대$(\infty)$까지의 값을 가질 수 있다.

로지스틱 회귀분석 | DataLatte’s IT Blog

로지스틱 회귀분석 로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다. 로지스틱 회귀분석 모형에서는 종속변수가 이항분포를 따르고 그 모수 $ \theta $ 가 독립변수 $ x $ 에 의존한다고 가정한다. p(y \mid x) = \text{Bin} (y; \theta (x), N) 위 식에

  • Image source: heung-bae-lee.github.io
  • Views: 102136
  • Publish date: 2 hours ago
  • Downloads: 35324
  • Likes: 6918
  • Dislikes: 3
로지스틱 회귀분석 | Datalatte'S It Blog
로지스틱 회귀분석 | Datalatte’S It Blog

그레디언트 벡터가 영벡터가 되는 모수의 값이 로그가능도를 최대화하는 값이다. 하지만 그레디언트 벡터 수식이 $ w $ 에 대한 비선형 함수이므로 선형모형과 같이 간단하게 그레디언트가 0이 되는 모수 $ w $ 값에 대한 수식을 구할 수 없으며 수치적인 최적화 방법(numerical optimization)을 통해 반복적으로 최적 모수 $ w $ 의 값을 구해야 한다.

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

0부터 1사이의 값만 가지는 확률값인 $ \theta (x) $ 를 오즈비로 변환하면 0부터 양의 무한대까지의 값을 가질 수 있다. 오즈비를 로그변환한 것이 위에서 언급한 Logit function이다. 이로써 로지트 함수의 값은 로그변환에 의해 음의 무한대 $(- \infty)$부터 양의 무한대$(\infty)$까지의 값을 가질 수 있다.

제13장 로지스틱회귀분석. – ppt download

로지스틱회귀분석 로지스틱회귀분석(logistic regression) 독립변수의 선형결합을 이용하여 사건의 발생가능성(발생확률)을 예측하는데 사용되는 통계기법 독립변수의 선형결합으로 종속변수를 설명한다는 관점에서는 회귀분석, 판별분석과 유사함 종속변수는 명목척도로서 binary data이어야 함 <참고> 종속변수 독립변수 분산분석 간격/비율척도 명목척도 회귀분석 간격/비율척도 명목/서열/간격/비율척도 판별분석 명목척도 명목/서열/간격/비율척도 로지스틱회귀분석 명목척도 (binary) 명목/서열/간격/비율척도

  • Image source: slidesplayer.org
  • Views: 3817
  • Publish date: 5 hours ago
  • Downloads: 90276
  • Likes: 2433
  • Dislikes: 6
제13장 로지스틱회귀분석. - Ppt Download
제13장 로지스틱회귀분석. – Ppt Download

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

고장률 failure rate 어떤 시점까지 동작하여 온 품목이 계속되는 단위기간내에 고장을 일으키는 비율(횟수). 고장률은 확률이 아니며 따라서 1 보다 커도 상관없다. 고장이 발생하기 쉬운 정도를 표시하는 척도. 일반으로 고장률은 순간고장률과 평균고장률을 사용하고 있지만.

10-7 부동소수점 (Floating-Point) 계산  컴퓨터에서 숫자를 표기하는 방법  가수 (Fraction) : 부호화된 고정소수점 숫자 지수 (Exponent) : 소수점의 위치를 표시 ( 예 )10 진수 를 표기하면 Fraction Exponent.

로지스틱 회귀분석 | DataLatte’s IT Blog

로지스틱 회귀분석 로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다. 로지스틱 회귀분석 모형에서는 종속변수가 이항분포를 따르고 그 모수 $ \theta $ 가 독립변수 $ x $ 에 의존한다고 가정한다. p(y \mid x) = \text{Bin} (y; \theta (x), N) 위 식에

  • Image source: heung-bae-lee.github.io
  • Views: 102556
  • Publish date: 2 hours ago
  • Downloads: 89039
  • Likes: 8045
  • Dislikes: 1
로지스틱 회귀분석 | Datalatte'S It Blog
로지스틱 회귀분석 | Datalatte’S It Blog

그레디언트 벡터가 영벡터가 되는 모수의 값이 로그가능도를 최대화하는 값이다. 하지만 그레디언트 벡터 수식이 $ w $ 에 대한 비선형 함수이므로 선형모형과 같이 간단하게 그레디언트가 0이 되는 모수 $ w $ 값에 대한 수식을 구할 수 없으며 수치적인 최적화 방법(numerical optimization)을 통해 반복적으로 최적 모수 $ w $ 의 값을 구해야 한다.

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

0부터 1사이의 값만 가지는 확률값인 $ \theta (x) $ 를 오즈비로 변환하면 0부터 양의 무한대까지의 값을 가질 수 있다. 오즈비를 로그변환한 것이 위에서 언급한 Logit function이다. 이로써 로지트 함수의 값은 로그변환에 의해 음의 무한대 $(- \infty)$부터 양의 무한대$(\infty)$까지의 값을 가질 수 있다.

6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨

  • Image source: datascienceschool.net
  • Views: 40262
  • Publish date: 4 hours ago
  • Downloads: 27192
  • Likes: 5657
  • Dislikes: 8
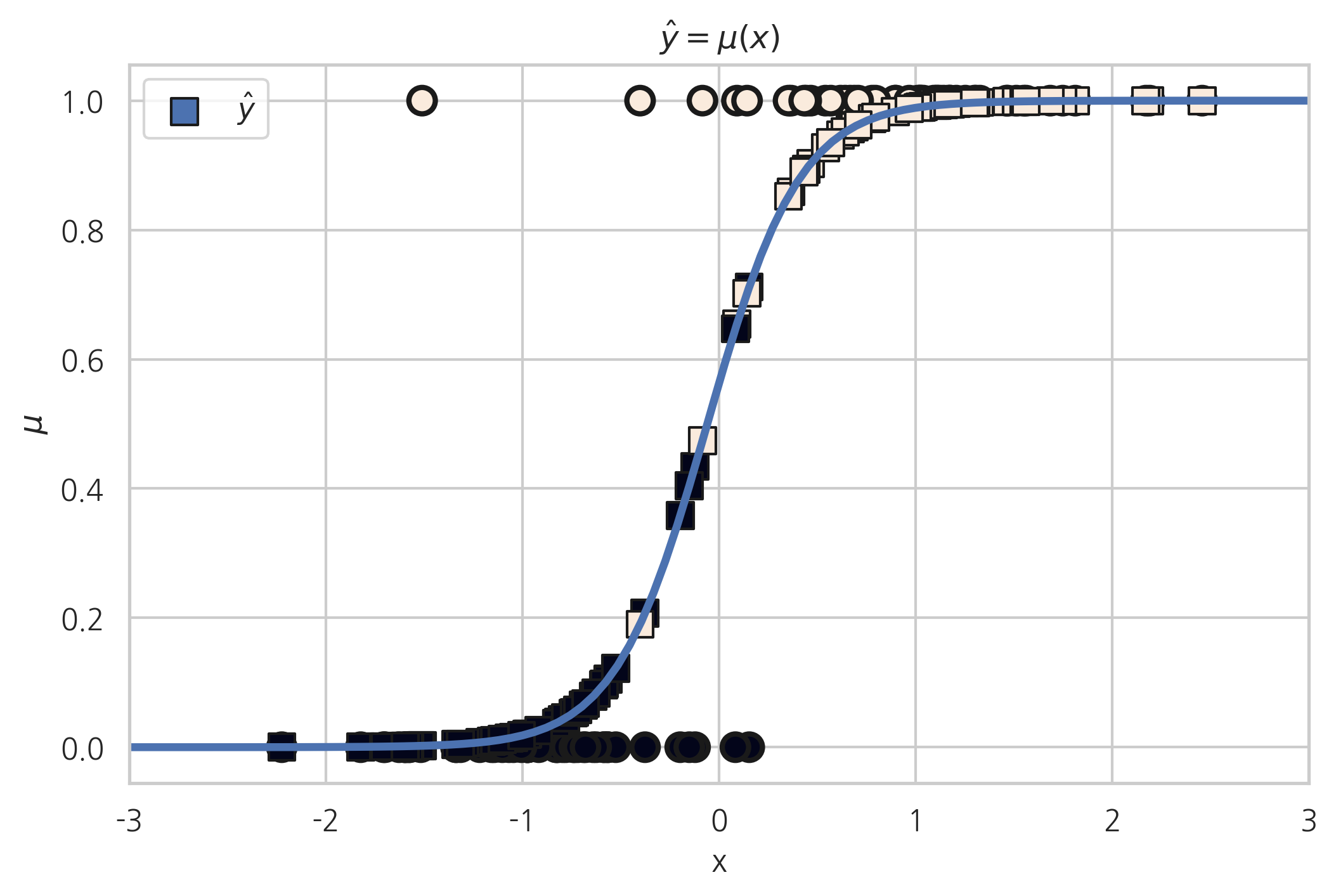
6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨
6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

붓꽃 분류문제에서 클래스가 베르시칼라(versicolor)와 버지니카(virginica) 데이터만 사용하여(versicolor=1, virginica=2) 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 독립변수는 모두 사용한다. 이 보고서에서 버지니카와 베르시칼라를 구분하는 경계면의 방정식을 찾아라.

&=& \sum_{i=1}^N \left( y_i \log\left(\dfrac{1}{1 + \exp{(-w^Tx_i)}}\right) + (1-y_i)\log\left(\dfrac{\exp{(-w^Tx_i)}}{1 + \exp{(-w^Tx_i)}}\right) \right) \\

로지스틱 회귀분석 | DataLatte’s IT Blog

로지스틱 회귀분석 로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다. 로지스틱 회귀분석 모형에서는 종속변수가 이항분포를 따르고 그 모수 $ \theta $ 가 독립변수 $ x $ 에 의존한다고 가정한다. p(y \mid x) = \text{Bin} (y; \theta (x), N) 위 식에

  • Image source: heung-bae-lee.github.io
  • Views: 78154
  • Publish date: 20 hours ago
  • Downloads: 81184
  • Likes: 5353
  • Dislikes: 6
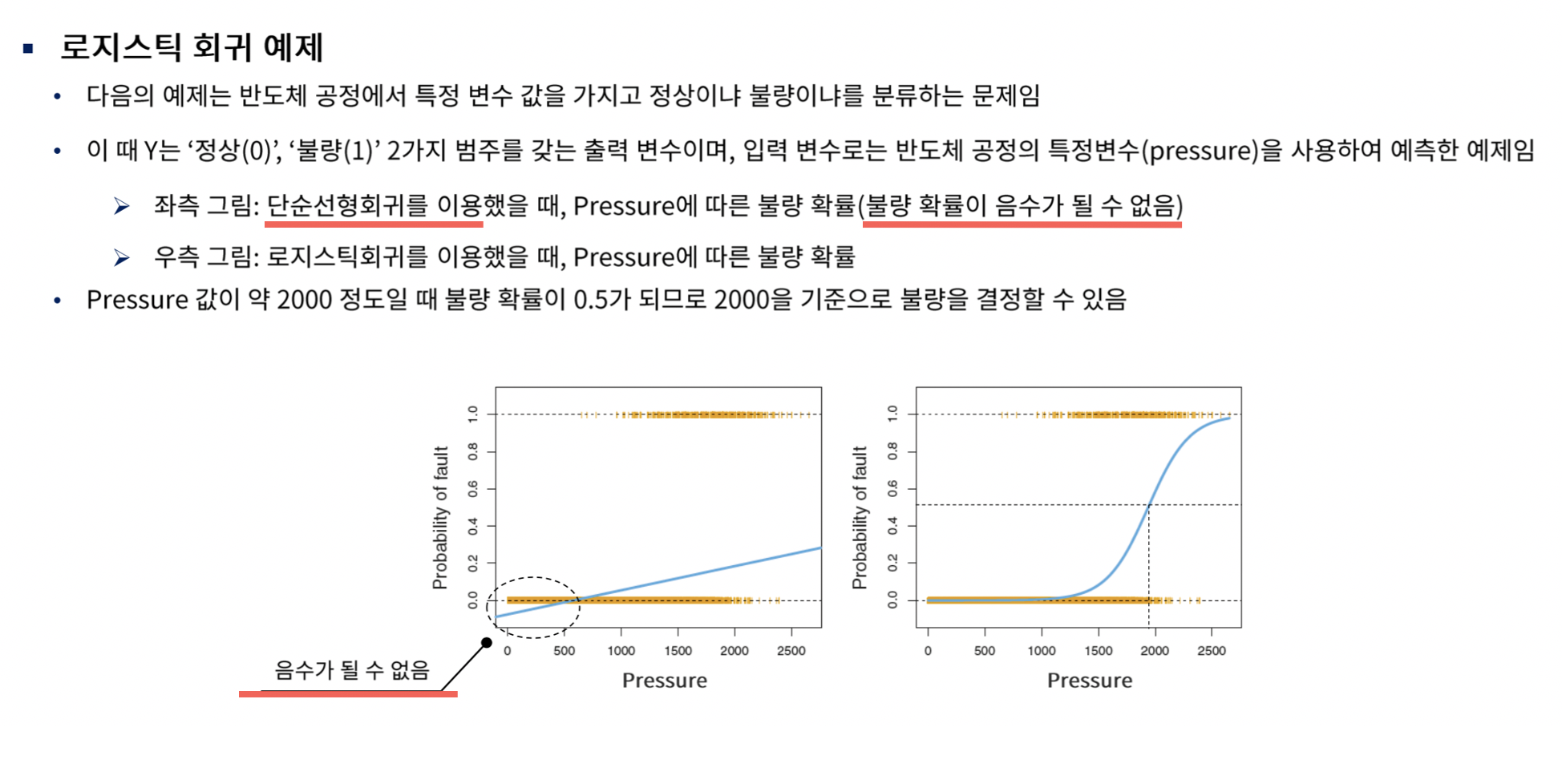
로지스틱 회귀분석 | Datalatte'S It Blog
로지스틱 회귀분석 | Datalatte’S It Blog

그레디언트 벡터가 영벡터가 되는 모수의 값이 로그가능도를 최대화하는 값이다. 하지만 그레디언트 벡터 수식이 $ w $ 에 대한 비선형 함수이므로 선형모형과 같이 간단하게 그레디언트가 0이 되는 모수 $ w $ 값에 대한 수식을 구할 수 없으며 수치적인 최적화 방법(numerical optimization)을 통해 반복적으로 최적 모수 $ w $ 의 값을 구해야 한다.

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

0부터 1사이의 값만 가지는 확률값인 $ \theta (x) $ 를 오즈비로 변환하면 0부터 양의 무한대까지의 값을 가질 수 있다. 오즈비를 로그변환한 것이 위에서 언급한 Logit function이다. 이로써 로지트 함수의 값은 로그변환에 의해 음의 무한대 $(- \infty)$부터 양의 무한대$(\infty)$까지의 값을 가질 수 있다.

6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨

  • Image source: datascienceschool.net
  • Views: 20524
  • Publish date: 7 hours ago
  • Downloads: 58275
  • Likes: 9601
  • Dislikes: 1
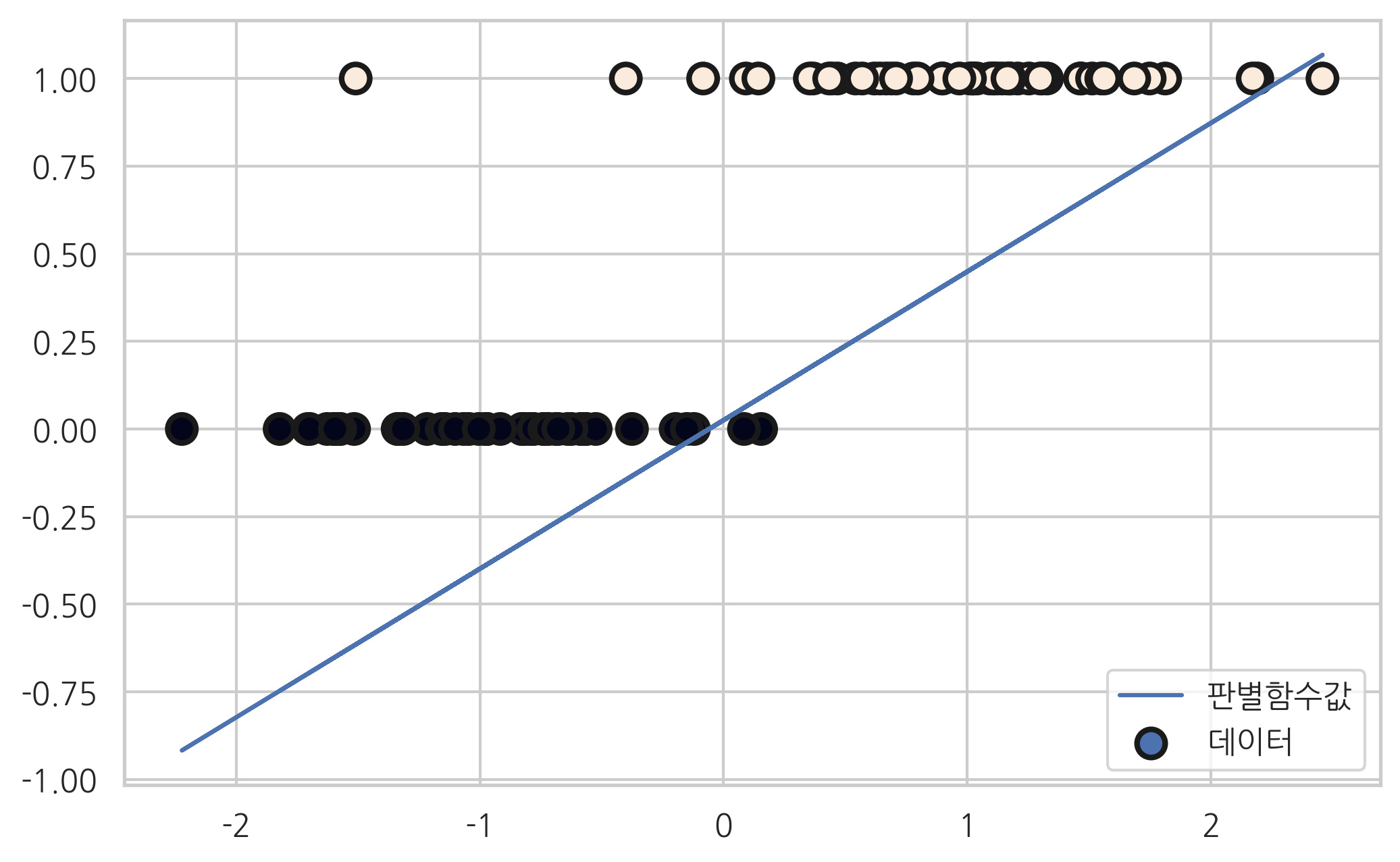
6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨
6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

붓꽃 분류문제에서 클래스가 베르시칼라(versicolor)와 버지니카(virginica) 데이터만 사용하여(versicolor=1, virginica=2) 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 독립변수는 모두 사용한다. 이 보고서에서 버지니카와 베르시칼라를 구분하는 경계면의 방정식을 찾아라.

&=& \sum_{i=1}^N \left( y_i \log\left(\dfrac{1}{1 + \exp{(-w^Tx_i)}}\right) + (1-y_i)\log\left(\dfrac{\exp{(-w^Tx_i)}}{1 + \exp{(-w^Tx_i)}}\right) \right) \\

로지스틱 회귀분석 | DataLatte’s IT Blog

로지스틱 회귀분석 로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다. 로지스틱 회귀분석 모형에서는 종속변수가 이항분포를 따르고 그 모수 $ \theta $ 가 독립변수 $ x $ 에 의존한다고 가정한다. p(y \mid x) = \text{Bin} (y; \theta (x), N) 위 식에

  • Image source: heung-bae-lee.github.io
  • Views: 68488
  • Publish date: 44 minute ago
  • Downloads: 80430
  • Likes: 2730
  • Dislikes: 10
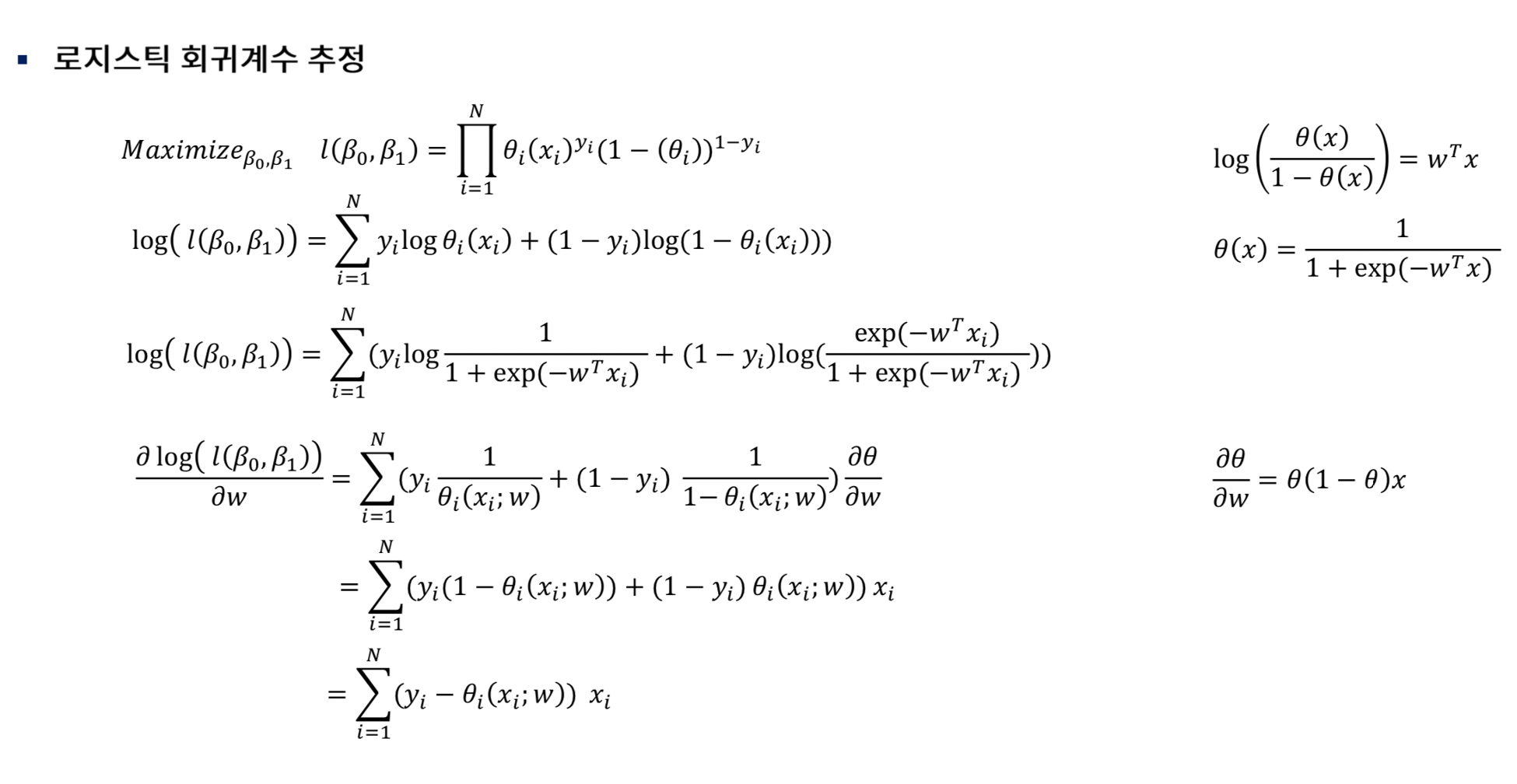
로지스틱 회귀분석 | Datalatte'S It Blog
로지스틱 회귀분석 | Datalatte’S It Blog

그레디언트 벡터가 영벡터가 되는 모수의 값이 로그가능도를 최대화하는 값이다. 하지만 그레디언트 벡터 수식이 $ w $ 에 대한 비선형 함수이므로 선형모형과 같이 간단하게 그레디언트가 0이 되는 모수 $ w $ 값에 대한 수식을 구할 수 없으며 수치적인 최적화 방법(numerical optimization)을 통해 반복적으로 최적 모수 $ w $ 의 값을 구해야 한다.

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

0부터 1사이의 값만 가지는 확률값인 $ \theta (x) $ 를 오즈비로 변환하면 0부터 양의 무한대까지의 값을 가질 수 있다. 오즈비를 로그변환한 것이 위에서 언급한 Logit function이다. 이로써 로지트 함수의 값은 로그변환에 의해 음의 무한대 $(- \infty)$부터 양의 무한대$(\infty)$까지의 값을 가질 수 있다.

범주화하기: 로지스틱 회귀, r 통계 분석

로지스틱 회귀(Logistic Regression)란 로지스틱 회귀란 한 변인 내 점수들을 기반으로 두 개의 범주 (이분 변인) 중 하나로 예측할 때 사용되는 통계 기법이다. 즉 종속변인이 이분변수일 경우 사용되는 회귀분석이라고 생각하면 쉽다. 다른 회귀분석처럼 로지스틱 회귀도 "예측적(predictive)" 분석기법이며, 독립변수와 종속변수 간의 관계를 설명해주는 분석기법이라 할 수 있다. 이 때 독립변수는 하나 이상의 명목, 서열, 동간, 비율 척도로 이루어진다. 이 때 중요한 점은 선형회귀에서는 종속 변수의 예측된 값이 독립변수들의 조합을 기반으로 한다는 점이다. 즉, 독립변수 x의 함수를 통해 조건 확률 Pr(Y = 1|X = x)을 모형화하여야 한다. 이 때 여러 알려지지 않은 변수들은 최대우도..

  • Image source: daily1123.tistory.com
  • Views: 86711
  • Publish date: 6 hours ago
  • Downloads: 23178
  • Likes: 4840
  • Dislikes: 9
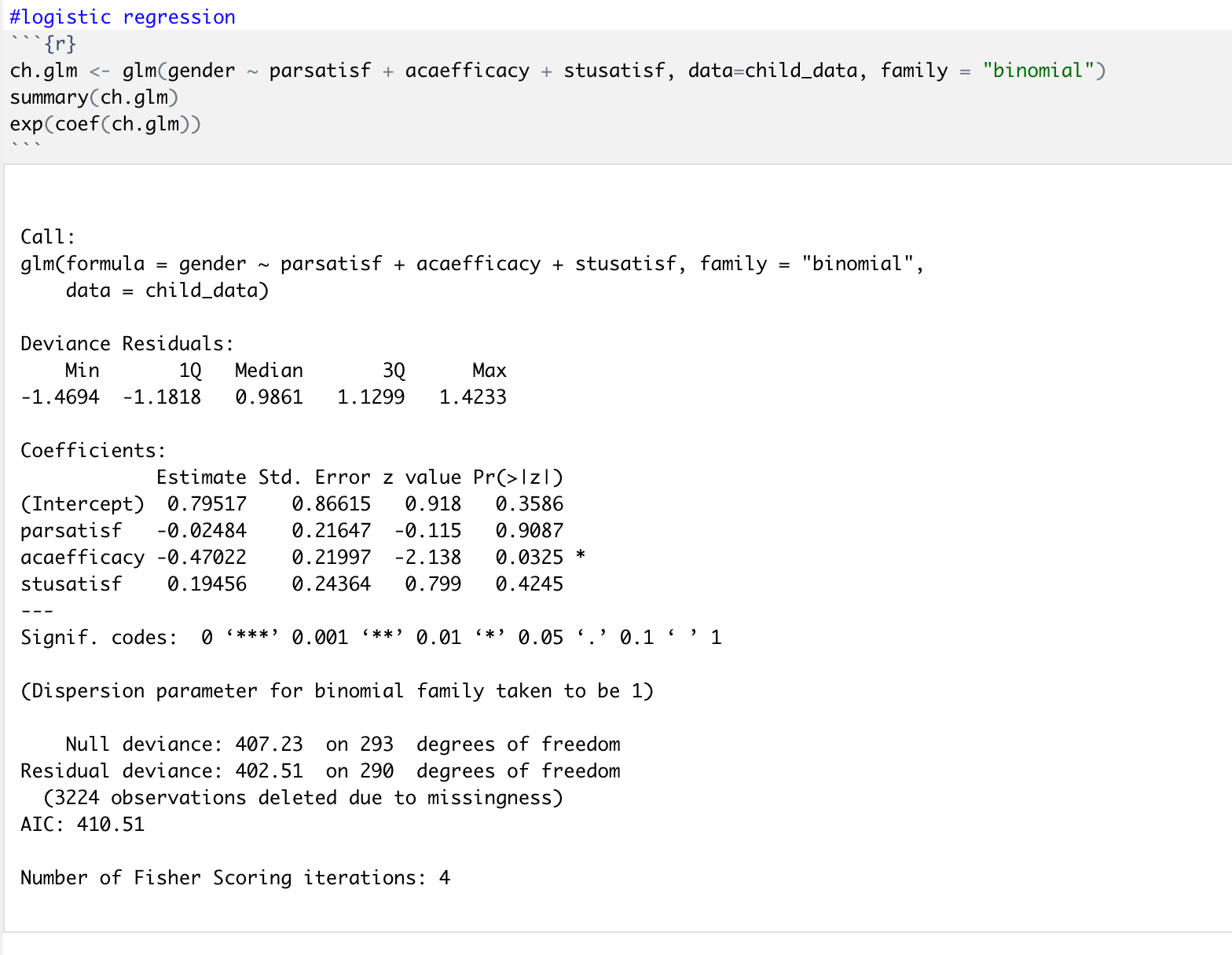
범주화하기: 로지스틱 회귀, R 통계 분석
범주화하기: 로지스틱 회귀, R 통계 분석

한 변인 내 점수들을 기반으로 두 개의 범주 (이분 변인) 중 하나로 예측할 때 사용되는 통계 기법이다. 즉 종속변인이 이분변수일 경우 사용되는 회귀분석이라고 생각하면 쉽다. 다른 회귀분석처럼 로지스틱 회귀도 “예측적(predictive)” 분석기법이며, 독립변수와 종속변수 간의 관계를 설명해주는 분석기법이라 할 수 있다. 이 때 독립변수는 하나 이상의 명목, 서열, 동간, 비율 척도로 이루어진다.

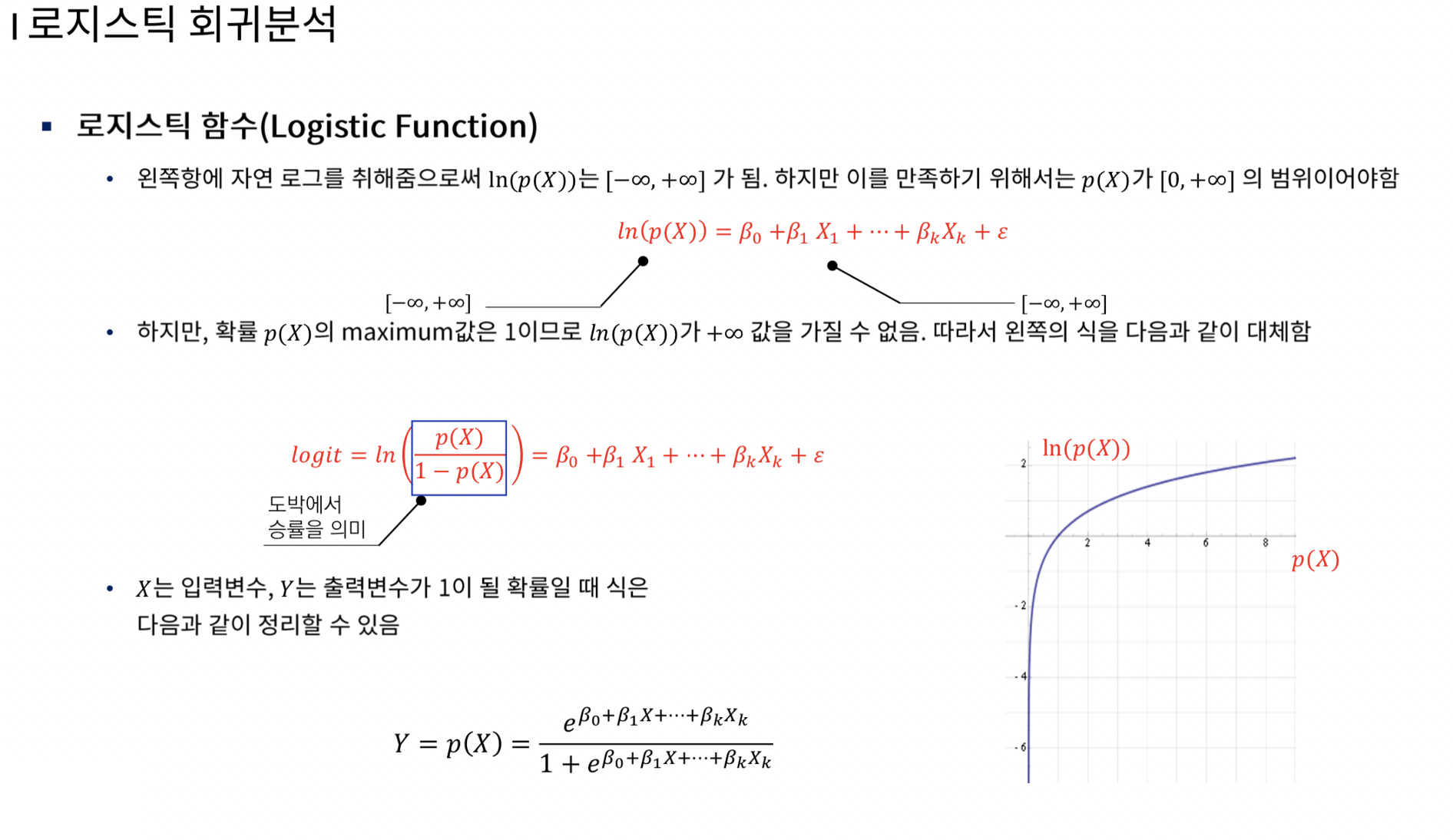
p(x)가 x의 선형함수가 되게 해보자. 이때 x가 증가 혹은 감소함에 따라 그만큼 확률도 변화하게 되는데, 이 때의 문제는 p가 0과 1 사이어야 하며, 선형 함수로 제한되지 않는다. 또 p가 변화함에 따라 같은 양만큼의 x도 변화되어야 하는데, p가 1/2에서 가까울 때보다 멀리 있는 경우 더 큰 변화가 나타난다. 따라서 이 방식은 선형 모형을 사용할 수 없다.

따라서 통계학자들은 log를 사용하여 log p(x)가 x의 선형함수가 되는 방식을 사용하였는데, 이는 p가 변화함에 따라 고정된 양만큼 x도 변화할 수 있게 해주었다. 하지만 로그는 하나의 방향으로만 무한대로 나타나기 때문에 양방향으로 무한대로 나타나는 선형 회귀를 그대로 사용할 수 없었다. 따라서 통계학자들은 log 1-p를 함께 사용하게 되었다.

6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨

  • Image source: datascienceschool.net
  • Views: 39961
  • Publish date: 53 minute ago
  • Downloads: 53630
  • Likes: 5215
  • Dislikes: 2
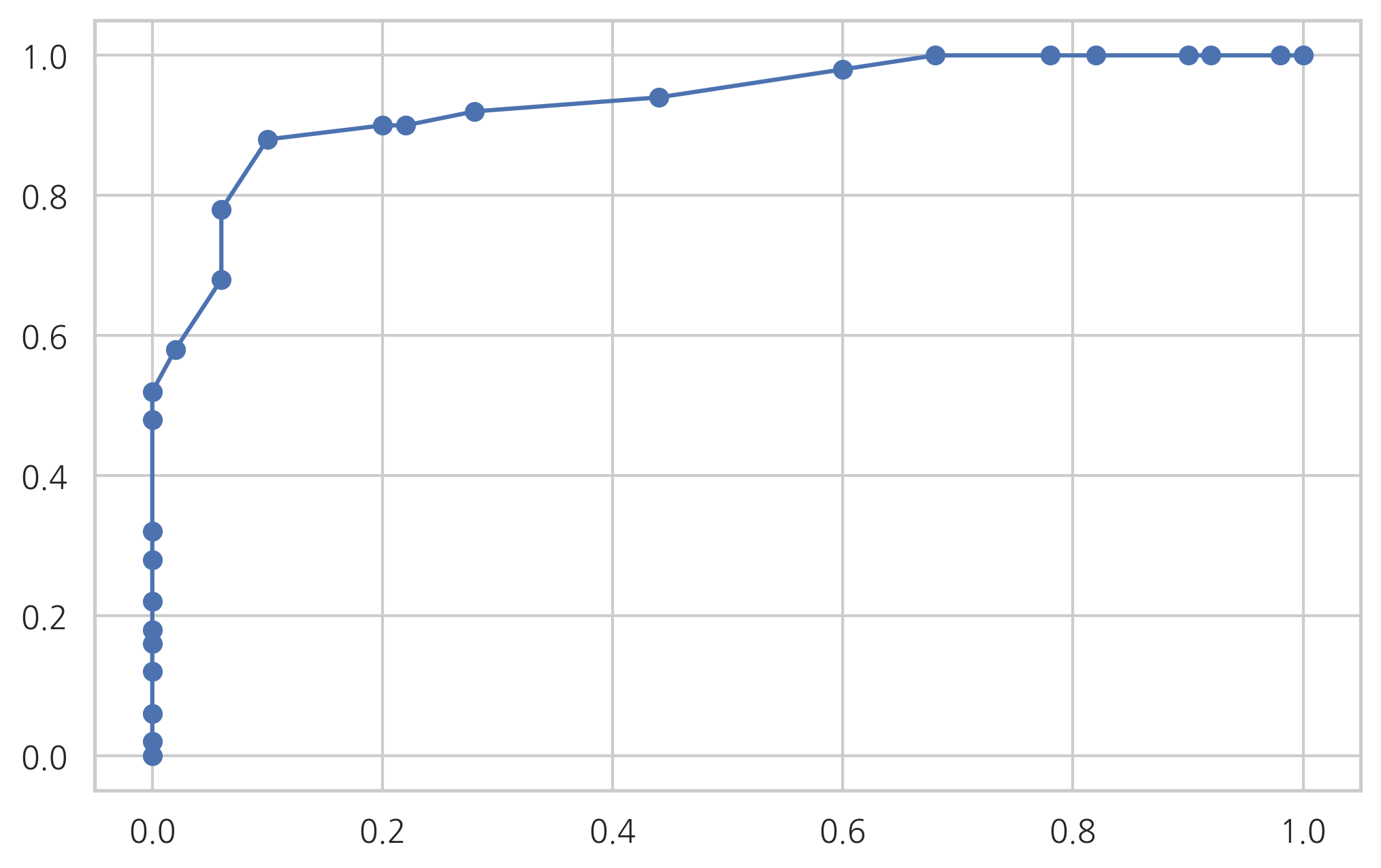
6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨
6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨

붓꽃 분류문제에서 클래스가 세토사와 베르시칼라 데이터만 사용하고 (setosa=0, versicolor=1) 독립변수로는 꽃받침 길이(Sepal Length)와 상수항만 사용하여 StatsModels 패키지의 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 이 보고서에서 어떤 값이 세토사와 베르시칼라를 구분하는 기준값(threshold)으로 사용되고 있는가?

붓꽃 분류문제에서 클래스가 베르시칼라(versicolor)와 버지니카(virginica) 데이터만 사용하여(versicolor=1, virginica=2) 로지스틱 회귀모형으로 결과를 예측하고 보고서를 출력한다. 독립변수는 모두 사용한다. 이 보고서에서 버지니카와 베르시칼라를 구분하는 경계면의 방정식을 찾아라.

&=& \sum_{i=1}^N \left( y_i \log\left(\dfrac{1}{1 + \exp{(-w^Tx_i)}}\right) + (1-y_i)\log\left(\dfrac{\exp{(-w^Tx_i)}}{1 + \exp{(-w^Tx_i)}}\right) \right) \\

제 2 장 회귀분석 동아대학교 경영정보학과 이정형. – ppt download

  • Image source: slidesplayer.org
  • Views: 33728
  • Publish date: 17 minute ago
  • Downloads: 87622
  • Likes: 1313
  • Dislikes: 5
제 2 장 회귀분석 동아대학교 경영정보학과 이정형. - Ppt Download
제 2 장 회귀분석 동아대학교 경영정보학과 이정형. – Ppt Download

수요 예측 2. 수요예측모형 신제품 또는 시장진입 초기제품일 경우 시장전략상 신상품에 대한 성장잠재기를 갖게 되므로 이 기간 동안은 전체적 구조가 S자형 곡선으로 나타남 따라서 수요확산 모형의 일종인 시간경향 모형법 (Time Trend Model)을 적용하여 수요를 예측 시간경향 모형법 : 자료가 시간에 따른 뚜렷한 경향을 지니고 있을 때 주로 사용하는 방법으로 산업구조의 변화와 같이 일정한 추세를 보이는 자료의 예측에 적합 시간경향 모형법은 시간적인 경향만을 추출해 내기 때문에 전 시점의 자료의 급작스런 감소나 증가에 영향을 받지 않아 예측 오차가 생길 우려가 있음 정확한 예측을 위해 시간 경향을 제거한 자료에 대하여 자기회귀 모형법 (Autoregre- ssive Model)을 적용하는 STEPAR법 (Stepwise Autoregressive Method)의 기본 모형식을 기반으로 계수 형태를 추정하여 모형을 완성 추정된 모형을 기초로 초고층 아파트의 건설현황을 연도별로 예측

예제) La Quinta Motor Inn을 위한 입지선택 분산분석표 회귀계수의 추정 Source DF Sum of Squares Mean Square F Value Pr > F Model 6 3123.8 520.64 17.14 <.0001 Error 93 2825.6 30.38 Total 99 5949.5 Variable Label DF Parameter Estimate Standard Error t Value Pr > |t| Intercept 1 38.1386 6.993 5.45 <.0001 x1 Nearest -0.0076 0.0013 -6.07 x2 Office 1.6462 0.6328 2.6 0.0108 x3 Space 0.0198 0.0034 5.8 x4 Enrollment 0.2118 0.1334 1.59 0.1159 x5 Income 0.4131 0.1396 2.96 0.0039 x6 Distance -0.2253 0.1787 -1.26 0.2107

예제) 패스트푸드 레스토랑의 입지 선택 분산분석표 회귀계수의 추정(VIF 포함) Source DF Sum of Squares Mean Square F Value Pr > F Model 5 368140 73628 36.86 <.0001 Error 19 37956 1997.7 Total 24 406096 Variable DF Parameter Estimate Standard Error t Value Pr > |t| VIF Intercept 1 -1134 320.02 -3.54 0.0022 Income 173.2 28.204 6.14 <.0001 226.82 Age 23.55 32.234 0.73 0.4739 101.28 Incomesq -3.726 0.5422 -6.87 191.38 Agesq -3.869 1.1791 -3.28 0.0039 46.316 (Income)(Age) 1.9673 0.9441 2.08 0.0509 56.509

제13장 로지스틱회귀분석. – ppt download

로지스틱회귀분석 로지스틱회귀분석(logistic regression) 독립변수의 선형결합을 이용하여 사건의 발생가능성(발생확률)을 예측하는데 사용되는 통계기법 독립변수의 선형결합으로 종속변수를 설명한다는 관점에서는 회귀분석, 판별분석과 유사함 종속변수는 명목척도로서 binary data이어야 함 <참고> 종속변수 독립변수 분산분석 간격/비율척도 명목척도 회귀분석 간격/비율척도 명목/서열/간격/비율척도 판별분석 명목척도 명목/서열/간격/비율척도 로지스틱회귀분석 명목척도 (binary) 명목/서열/간격/비율척도

  • Image source: slidesplayer.org
  • Views: 49666
  • Publish date: 44 minute ago
  • Downloads: 103918
  • Likes: 5609
  • Dislikes: 10
제13장 로지스틱회귀분석. - Ppt Download
제13장 로지스틱회귀분석. – Ppt Download

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

고장률 failure rate 어떤 시점까지 동작하여 온 품목이 계속되는 단위기간내에 고장을 일으키는 비율(횟수). 고장률은 확률이 아니며 따라서 1 보다 커도 상관없다. 고장이 발생하기 쉬운 정도를 표시하는 척도. 일반으로 고장률은 순간고장률과 평균고장률을 사용하고 있지만.

10-7 부동소수점 (Floating-Point) 계산  컴퓨터에서 숫자를 표기하는 방법  가수 (Fraction) : 부호화된 고정소수점 숫자 지수 (Exponent) : 소수점의 위치를 표시 ( 예 )10 진수 를 표기하면 Fraction Exponent.

비디오 로지스틱 회귀분석 해석 로지스틱 회귀분석 해석 방법 / 논문 통계 표 양식 / 이항 로짓 / Exp(b) / 논문쓰는남자 / 논쓰남

  • Source: Youtube
  • Views: 53011
  • Date: 46 minute ago
  • Download: 82157
  • Likes: 8884
  • Dislikes: 1

주제에 대한 관련 정보 로지스틱 회귀분석 해석

Bing에서 로지스틱 회귀분석 해석 주제에 대한 최신 정보를 볼 수 있습니다.

로지스틱 회귀분석 해석 in r

python 로지스틱 회귀분석 해석

다항 로지스틱 회귀분석 해석

spss 로지스틱 회귀분석 해석

로지스틱 회귀분석 예제

로지스틱 회귀분석 오즈비 해석

stata 로지스틱 회귀분석 해석

로지스틱 회귀분석 논문 표

주제에 대한 기사 보기를 마쳤습니다 로지스틱 회귀분석 해석. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.

로지스틱 회귀분석 해석 in r

python 로지스틱 회귀분석 해석

다항 로지스틱 회귀분석 해석

spss 로지스틱 회귀분석 해석

로지스틱 회귀분석 예제

로지스틱 회귀분석 오즈비 해석

stata 로지스틱 회귀분석 해석

로지스틱 회귀분석 논문 표

Leave a Comment