베스트 1075 사인 코사인 법칙 업데이트 184 시간 전

by

사인 코사인 공식

사인 코사인 변환

삼각함수 사인 코사인 법칙

제2 코사인법칙

제1코사인법칙

제이코사인법칙

사인법칙 내접원

코사인법칙 공식

주제에 대한 기사를 찾고 있습니까 “사인 코사인 법칙“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: 974 사진을 다운로드할 수 있는 최고의 웹사이트. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.

이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.

컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.

사인 코사인 법칙 주제와 관련된 상위 91 이미지

주제 사인 코사인 법칙 와 관련된 22 개의 이미지가 있습니다.

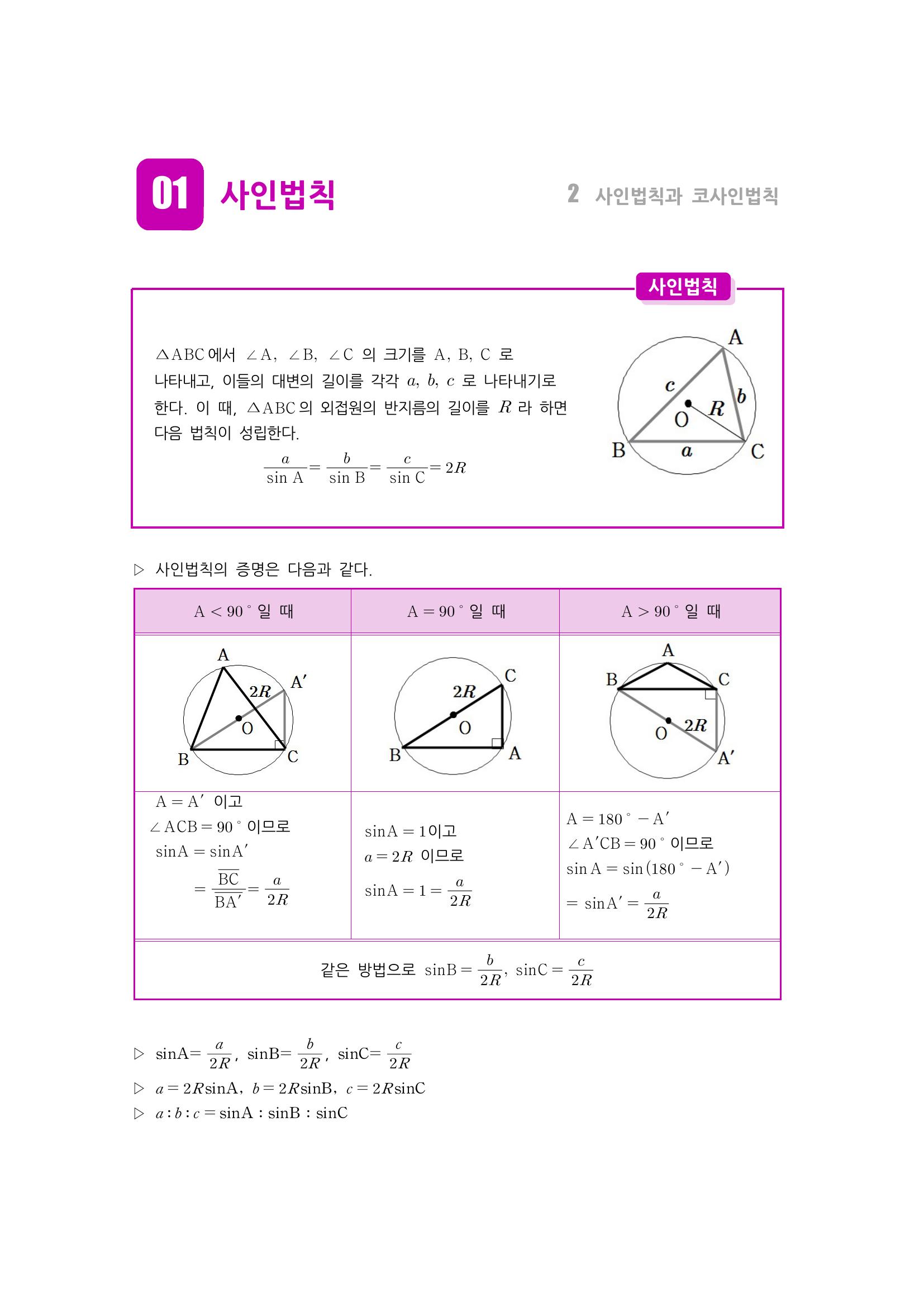
수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙

  • Image source: koreanfoodie.me
  • Views: 56492
  • Publish date: 4 hours ago
  • Downloads: 84799
  • Likes: 4082
  • Dislikes: 9
수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙
수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙

수학 개념 정리/공식 : 수열, 등차수열, 등차수열의 일반항, 등차중항, 등차수열의 합, 등비수열, 등비수열의 일반항, 등비중항, 등비수열의 합

수학 개념 정리/공식 : 수열, 등차수열, 등차수열의 일반항, 등차중항, 등차수열의 합, 등비수열, 등비수열의 일반항, 등비중항, 등비수열의 합

수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙 본문

수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙

  • Image source: koreanfoodie.me
  • Views: 13779
  • Publish date: 6 hours ago
  • Downloads: 34629
  • Likes: 5005
  • Dislikes: 5
수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙
수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙

수학 개념 정리/공식 : 수열, 등차수열, 등차수열의 일반항, 등차중항, 등차수열의 합, 등비수열, 등비수열의 일반항, 등비중항, 등비수열의 합

수학 개념 정리/공식 : 수열, 등차수열, 등차수열의 일반항, 등차중항, 등차수열의 합, 등비수열, 등비수열의 일반항, 등비중항, 등비수열의 합

수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙 본문

사인법칙 간단하게 이해하기 : 네이버 블로그

수학 공식은 암기해야 하는 부분이 분명 있지만 암기하지 않고도 '스스로' 생각해낸 경험이 있다…

  • Image source: m.blog.naver.com
  • Views: 38753
  • Publish date: 21 minute ago
  • Downloads: 65908
  • Likes: 2736
  • Dislikes: 2
사인법칙 간단하게 이해하기 : 네이버 블로그
사인법칙 간단하게 이해하기 : 네이버 블로그

그 세 점을 서로 이어 삼각형을 만들면 이는 평면상의 삼각형이고, 그 삼각형을 내접삼각형으로 하는 외접원이 존재할 것이다.(이는 평면상의 원의 방정식이

곧, 세 각의 크기와 한 변만 알면 나머지 두 변의 길이를 구할 수 있다. (물론 계산할 수 있다는 말은 아님)

삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이)

안녕하세요. 훈릴스입니다. 오늘은 삼각함수의 공식 중 제 2 코사인 법칙에 대해 알아보는 시간을 가져보고자 합니다. 요즘들어 삼각함수와 관련된 포스팅을 많이하고 있는데요. 정말 해도해도 끝이없는 것이 수험생 여러분들의 고통이 느껴집니다. 간단하니, 따라오시죠! 레츠게릿 코사인 제 2법칙은 다음과 같습니다. 어려워보이지만 사실은 간단한데요. 우리가 구하고자하는 변의 제곱은 다른 변의 제곱의 합에서 다른 두변의 곱에 2를 곱하고 구하고자하는 변의 마주편 각의 Cos을 곱한 것과 같습니다. 말로 표현하자니 어렵지만, 열 번 정도 공책에 적어보시면 원리를 쉽게 익히실 수 있을 것입니다. 코사인 제 2법칙은 다양한 문제에 적용되기에 꼭 알고 계셔야하는데요. 공식만 알고가면 그러니, 바로 예제 문제 풀이를 해보겠습..

  • Image source: alive-earth.com
  • Views: 26814
  • Publish date: 5 hours ago
  • Downloads: 71130
  • Likes: 7214
  • Dislikes: 10
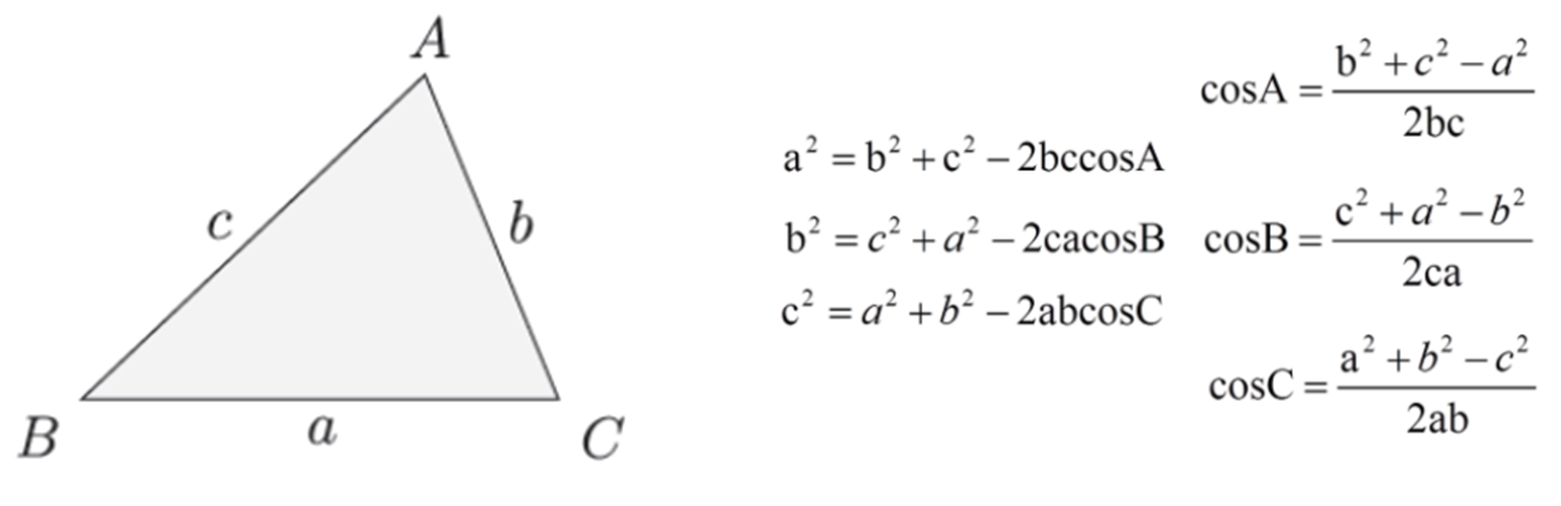
삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이)
삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이)

코사인 제 2법칙은 다음과 같습니다. 어려워보이지만 사실은 간단한데요. 우리가 구하고자하는 변의 제곱은 다른 변의 제곱의 합에서 다른 두변의 곱에 2를 곱하고 구하고자하는 변의 마주편 각의 Cos을 곱한 것과 같습니다. 말로 표현하자니 어렵지만, 열 번 정도 공책에 적어보시면 원리를 쉽게 익히실 수 있을 것입니다. 코사인 제 2법칙은 다양한 문제에 적용되기에 꼭 알고 계셔야하는데요. 공식만 알고가면 그러니, 바로 예제 문제 풀이를 해보겠습니다. 따라오시죠!

오늘은 삼각함수의 공식 중 제 2 코사인 법칙에 대해 알아보는 시간을 가져보고자 합니다. 요즘들어 삼각함수와 관련된 포스팅을 많이하고 있는데요. 정말 해도해도 끝이없는 것이 수험생 여러분들의 고통이 느껴집니다. 간단하니, 따라오시죠! 레츠게릿

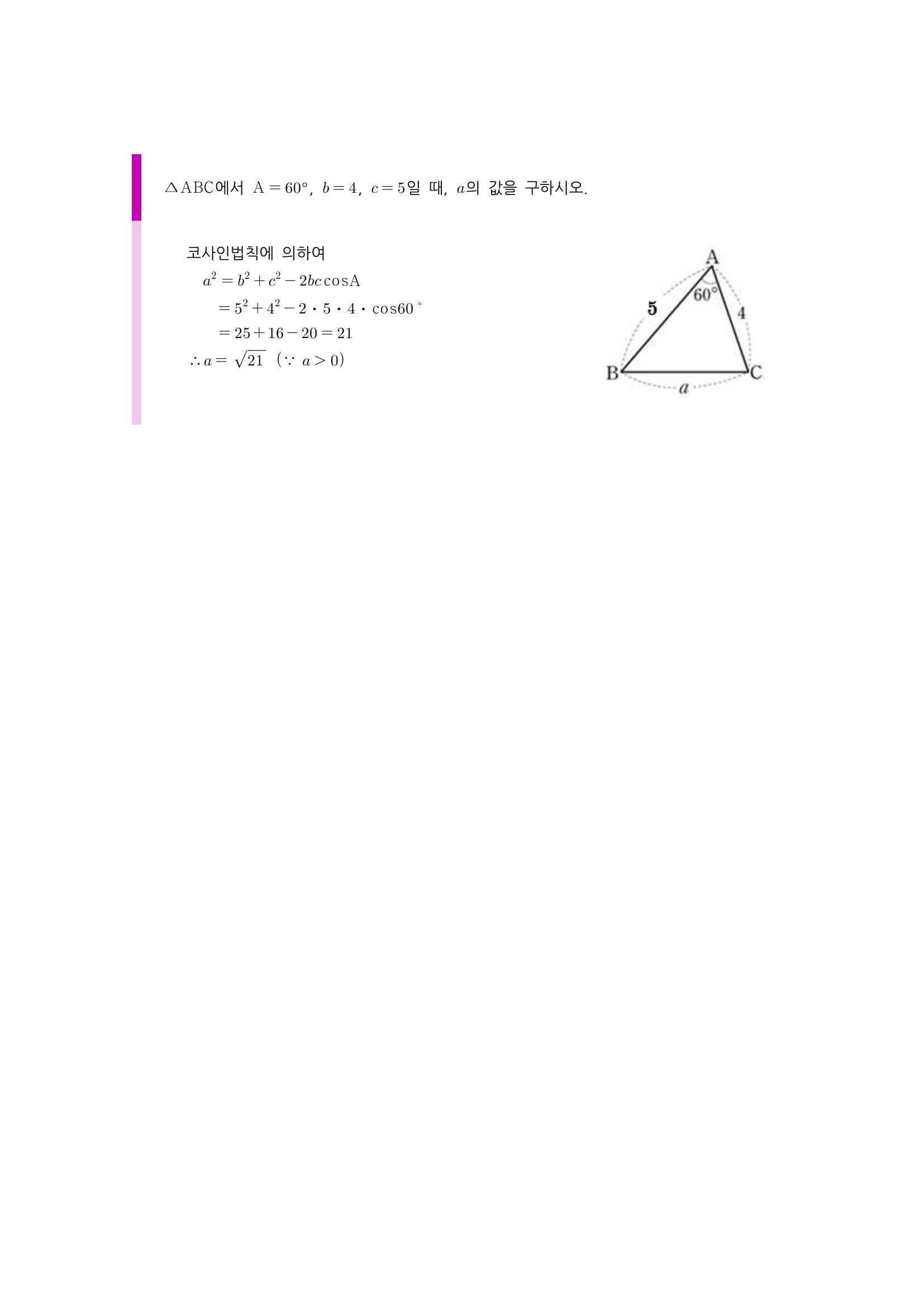
문제가 주어졌네요. 각 하나와 변의 길이가 두 개가 주어지면 코사인 2법칙을 이용해서 풀어야한다고 머릿속에서 생각하셔야 해요. 앞서 배운 공식을 적용해서 문제 풀이를 진행하면, 다음과 같습니다.

코사인법칙 핵꿀팁 – 오르비

세 변의 길이비가 4:5:6일 때, 제일 많이 출제되는 코사인값 3/4. , 1/8을 모두 가지고 있음 코사인이 1/2인 뻔한 문제가 아니라는 가정에서 가장 출제가능성이 높은 삼각형의 길이비 4:5:6 과 함께 코사인값 3/4와 1/8을 기억해놓자 솔직히 이건 좋아요 누르자

  • Image source: orbi.kr
  • Views: 80429
  • Publish date: 1 hours ago
  • Downloads: 3414
  • Likes: 4612
  • Dislikes: 5
코사인법칙 핵꿀팁 - 오르비
코사인법칙 핵꿀팁 – 오르비

문제 만들다보면 자주 쓰게되는 삼각비들이 있어요. 숫자 맞추기가 정말 편해서. 한 삼각형 안에서 돌고 도는 그런 비들이 ㅋㅋ. 대표적인걸로 (1/3, 2루트2/3)과 (7/9, 4루트2/9)가 있지용.. 코사인에 음수는 붙이든 말든해서뭐.. 삼각함수의 합성 이용해서 구해보면 자주나오는 비들의 이유를 알수 있습니다.. 수험생분들 알아놓으시면 나중에 도움될수도.. 권장은 하진 않지만

요샌 이런게 수능에 나와요? 저희땐 고1내용이라 코사인법칙이 출제 목적이 되진 않았었는데 삼각함수가 학년이 올라간건지

작수 수학 5등급인데 현우진 커리 탈꺼면 시발점+쎈 같이 나간뒤에 뉴런이랑 수분감 같이 나가면됨?

[수능특강 핵심정리 수학1] 4. 사인법칙과 코사인법칙 – 오르비

이 문제들은 배울거리가 있으니 풀어보시는게 좋지 않을까요?! 보통 시험은 다수의 정형적인 문제와 소수의 특이한 문제가 나오죠.  정형적인 문제에서 자주 중요하게 쓰이는 테크닉이 녹아든 문제 + 독특해서 한 번 짚고 넘어갈 문제를 골라봤습니다.   보시기전에 직접 풀어보시고, 영상을 통해 배울거리를 중심적으로 보시는게 좋겠죠?  [풀어볼 문제 +…

  • Image source: orbi.kr
  • Views: 74597
  • Publish date: 6 hours ago
  • Downloads: 14286
  • Likes: 7544
  • Dislikes: 4
수능특강 핵심정리 수학1] 4. 사인법칙과 코사인법칙 - 오르비
수능특강 핵심정리 수학1] 4. 사인법칙과 코사인법칙 – 오르비

66p Level2 9번 → 산술평균 기하평균 유의할 점(① 등호 조건 성립 여부, ② 한 쪽이 상수 나올 때 쓰기)

정형적인 문제에서 자주 중요하게 쓰이는 테크닉이 녹아든 문제 + 독특해서 한 번 짚고 넘어갈 문제를 골라봤습니다.

62p Level1 3번 → 직각 눈썰미(3:4:5, 5:12:13, 8:15:17, 7:24:25)

수학 – 수1 – 삼각함수- 오누이

  • Image source: onuii.com
  • Views: 54805
  • Publish date: 7 minute ago
  • Downloads: 59140
  • Likes: 8963
  • Dislikes: 3
수학 - 수1 - 삼각함수- 오누이
수학 – 수1 – 삼각함수- 오누이

사인법칙과 코사인법칙을 동시에 활용하는, 곱씹어 생각해 볼만한 좋은 문제입니다!

2022.03.07 11:23:22

오누이에 전과목 질문하러 가기

2021 EBS 수능특강 수학1 4. 사인법칙과 코사인법칙(2)

2021 EBS 수능특강 수학1 4. 사인법칙과 코사인법칙(2)

  • Image source: namuacademy.com
  • Views: 89197
  • Publish date: 8 hours ago
  • Downloads: 82546
  • Likes: 8194
  • Dislikes: 1
2021 Ebs 수능특강 수학1 4. 사인법칙과 코사인법칙(2)
2021 Ebs 수능특강 수학1 4. 사인법칙과 코사인법칙(2)

자유롭게 편집이 가능한 HWP 파일을 다운 받을 수 있습니다. 각 파일마다 해당 포인트를 지불하거나 HWP 프리패스를 구입하셔야 이용이 가능합니다.

[고2 내신] 고2 언어와 매체 비상 3. 단어와 음운의 탐구 및 활용 내신 대비 강의

2021 EBS 수능특강 수학1 4. 사인법칙과 코사인법칙2.hwp (321.0K)

수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙

  • Image source: koreanfoodie.me
  • Views: 80549
  • Publish date: 12 hours ago
  • Downloads: 93019
  • Likes: 3003
  • Dislikes: 8
수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙
수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙

수학 개념 정리/공식 : 수열, 등차수열, 등차수열의 일반항, 등차중항, 등차수열의 합, 등비수열, 등비수열의 일반항, 등비중항, 등비수열의 합

수학 개념 정리/공식 : 수열, 등차수열, 등차수열의 일반항, 등차중항, 등차수열의 합, 등비수열, 등비수열의 일반항, 등비중항, 등비수열의 합

수학 개념 정리/공식 : 사인법칙, 코사인법칙, 삼각형의 넓이, 제1 사인법칙, 제2사인법칙, 제1 코사인법칙, 제2 코사인 법칙 본문

사인법칙|샘토링 수학(samtoring)

사인법칙|샘토링 수학(samtoring)

  • Image source: samtoring.com
  • Views: 73952
  • Publish date: 16 hours ago
  • Downloads: 63865
  • Likes: 8288
  • Dislikes: 7
사인법칙|샘토링 수학(Samtoring)
사인법칙|샘토링 수학(Samtoring)

$\angle A = 60^\circ~ 또는 ~120^\circ , \angle C = 90^\circ ~또는 ~30^\circ$

#삼각형의 넓이 구하기 ( frac{1}{2} ab sin heta )

Ctrl+Shift+F : 문제 통합검색 창으로 포커스 이동

삼각함수 2

삼각함수의 이해 – 2 >> 사인법칙과 코사인법칙 – 삼각형에 대한 삼각함수의 활용 이제 삼각형에 대한 삼각함수의 활용을 간단히 알아보도록 하자. 임의의 삼각형에 대해서 두 개의 각을 알고 한 변의 길이를 알 때 나머지 두 변의 길이를 구하는 문제라든지, 두 변의 길이를 알고 그 끼인각의 크기를 알 때 나머지 한 변의 길이를 구하는 문제 등은 이른바 사인법칙과 코사인법칙이라고 불리는 삼각함수의 활용으로 해결할 수 있다. 그리고 코사인 법칙은 나중에 선형대수를 공부할 때, 벡터의 중요한 연산들 중 하나인 내적(Inner Product)이라는 연산을 정의하고 그 연산 결과를 증명하면서 다시 필요하게 될 것이므로 지금 잘 숙지해 두도록 하자. 그럼 이제 아래에서 사인법칙과 코사인법칙을 유도해 보겠다. >> 삼..

  • Image source: ncanis.tistory.com
  • Views: 30963
  • Publish date: 13 hours ago
  • Downloads: 873
  • Likes: 3176
  • Dislikes: 8
삼각함수 2
삼각함수 2

이제 삼각형에 대한 삼각함수의 활용을 간단히 알아보도록 하자. 임의의 삼각형에 대해서 두 개의 각을 알고 한 변의 길이를 알 때 나머지 두 변의 길이를 구하는 문제라든지, 두 변의 길이를 알고 그 끼인각의 크기를 알 때 나머지 한 변의 길이를 구하는 문제 등은 이른바 사인법칙과 코사인법칙이라고 불리는 삼각함수의 활용으로 해결할 수 있다. 그리고 코사인 법칙은 나중에 선형대수를 공부할 때, 벡터의 중요한 연산들 중 하나인 내적(Inner Product)이라는 연산을 정의하고 그 연산 결과를 증명하면서 다시 필요하게 될 것이므로 지금 잘 숙지해 두도록 하자. 그럼 이제 아래에서 사인법칙과 코사인법칙을 유도해 보겠다.

그리고 앞으로 진행될 선형대수 강좌와 3D그래픽스 응용에 있어서 지겹도록 사용하게 될 행렬들 중 하나가 바로 회전행렬인데, 이때가 되면 회전행렬을 구성하는 각 요소들은 결국 삼각함수에 대한 덧셈정리의 결과임을 자연스럽게 알게 될 것이다. 좌표축의 회전을 각도들의 덧셈으로 표현할 수 있음을 상기해보면 이는 너무나 당연한 결과이다. 따라서 덧셈정리 정도는 반사적으로 유도할 수 있도록 숙지해 두는 것이 앞으로의 학습에 여러모로 유리할 것이다.

학창시절 누구나 한번쯤은 삼각함수 항등식을 외우느라 골머리를 앓아본 적이 있을 것이다. 삼각함수 항등식은 여러 가지가 있지만, 본 절에서는 모든 항등식 유도의 기초가 되는 덧셈정리에 대해서 자세히 알아보도록 하겠다. 사실 대부분의 삼각함수 항등식은 덧셈정리로부터 간단히 유도되어 지거나 또는 그 유도에 있어서 덧셈정리의 결과가 유용하게 사용되어 진다는 사실을 본 절의 학습을 통해서 자연스럽게 알게 될 것이다.

삼각함수의 정의를 이용한 제2코사인 법칙 증명

proof of second law of cosines

  • Image source: freshrimpsushi.github.io
  • Views: 85234
  • Publish date: 9 hours ago
  • Downloads: 49051
  • Likes: 3521
  • Dislikes: 3
삼각함수의 정의를 이용한 제2코사인 법칙 증명
삼각함수의 정의를 이용한 제2코사인 법칙 증명

b^{2}+c^{2} &= (bc\cos\alpha + ab\cos\gamma) + (bc\cos\alpha + ac\cos\beta)

$\eqref{eq1}$, $\eqref{eq2}$, $\eqref{eq3}$을 묶어 제1 코사인 법칙이라 부르기도 한다.

\\ && \implies b^{2}&=bc\cos\alpha + ab\cos\gamma \nonumber

수학 – 수1 – 삼각함수- 오누이

  • Image source: onuii.com
  • Views: 102386
  • Publish date: 2 hours ago
  • Downloads: 104242
  • Likes: 455
  • Dislikes: 8
수학 - 수1 - 삼각함수- 오누이
수학 – 수1 – 삼각함수- 오누이

제2코사인 법칙과 삼각형의 넓이 공식을 사용하면 됩니다.

2018.12.15 12:27:32

오누이에 전과목 질문하러 가기

비디오 사인 코사인 법칙 사인법칙

  • Source: Youtube
  • Views: 74319
  • Date: 9 minute ago
  • Download: 20784
  • Likes: 3917
  • Dislikes: 2

주제에 대한 관련 정보 사인 코사인 법칙

Bing에서 사인 코사인 법칙 주제에 대한 최신 정보를 볼 수 있습니다.

사인 코사인 공식

사인 코사인 변환

삼각함수 사인 코사인 법칙

제2 코사인법칙

제1코사인법칙

제이코사인법칙

사인법칙 내접원

코사인법칙 공식

주제에 대한 기사 보기를 마쳤습니다 사인 코사인 법칙. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.

사인 코사인 공식

사인 코사인 변환

삼각함수 사인 코사인 법칙

제2 코사인법칙

제1코사인법칙

제이코사인법칙

사인법칙 내접원

코사인법칙 공식

Leave a Comment