초등 삼각형의 넓이 공식
삼각형 넓이 공식 모음
삼각형의 넓이 구하는 방법 5학년
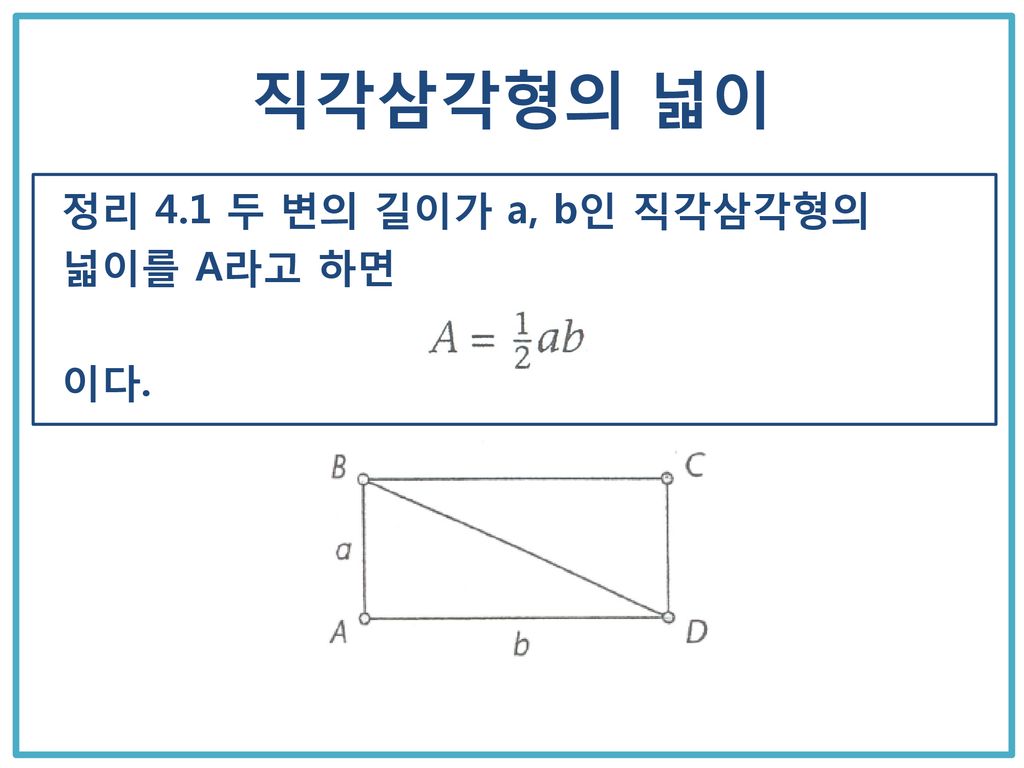
직각삼각형 넓이 구하는 방법
초등학교 삼각형 넓이
이등변삼각형 넓이 공식
삼각형의 넓이 sin
삼각형 넓이 공식 sin
주제에 대한 기사를 찾고 있습니까 “삼각형의 넓이 구하는 공식“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: 974 사진을 다운로드할 수 있는 최고의 웹사이트. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.
이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.
컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.
삼각형의 넓이 공식 모르는 사람 없죠? ½ × (밑변) × (높이)에요. 물론 이건 높이를 알고 있을 때 쓰는 공식이에요. 예각삼각형의 높이, 둔각삼각형의 높이에서도 해봤지만, 삼각비에는 변의 길이와 내각의 크기를 알려주지, 삼각형의 높이는 알려주지 않거든요.마름모의 넓이를 어떻게 구하는지 이야기해 보세요. 마름모를 잘라서 만든 평행사변형의 밑변의 길이와 높이를 곱합니다.
Table of Contents
삼각형의 넓이 구하는 공식 주제와 관련된 상위 40 이미지
주제 삼각형의 넓이 구하는 공식 와 관련된 17 개의 이미지가 있습니다.
세 점의 좌표로 삼각형의 넓이 구하는 공식 (사선공식, 신발끈공식)
학교에서는 안 알려주지만 학원에선 반드시 알려주는 공식들이 있죠. 오늘 다뤄볼 내용은 그 중 하나인 신발끈 공식입니다. 삼각형의 넓이를 구할 때, 세 점의 좌표로 바로 구할 수 있는 방법이에요. 내신에서 빈출되는 유형인데, 서술형으로 나오는 경우에는 문제의 의도와 맞지 않기 때문에 공식 쓰는 걸 인정 안해주는 게 일반적이긴 하죠. 그렇지만, 계산이 맞는지 검증하는 용도로 쓰면 되고, 객관식일 때는 시간을 많이 단축시켜주니 모르면 나만 손해겠죠? 신발끈 공식 위에도 썼지만, 신발끈 공식은 좌표평면 상에서 꼭짓점의 좌표를 알 때 다각형의 면적을 구할 수 있는 방법입니다. 이따 사용방법을 보면 알겠지만, 구할 때 삼각형의 각 꼭짓점의 좌푯값을 교차하여 곱하는 모습이 신발끈을 묶을 때와 같아 이러한 이름이 붙었..
- Image source: ladyang86.tistory.com
- Views: 28947
- Publish date: 20 hours ago
- Downloads: 52129
- Likes: 12
- Dislikes: 9

역사를 잠깐 살펴보자면, 신발끈 공식은 1769년에 수학자 마이스터 알베르트 루드비히 프레드리히(Meister Albrecht Ludwig Friedrich, 1724-1788)가 발견했으며, 1795년에 가우스도 독립적으로 발견하였습니다. 다각형을 여러 개의 삼각형으로 나누는 방식으로 증명할 수 있으며, 그린 정리의 특수한 형태로 볼 수도 있습니다.
위에도 썼지만, 신발끈 공식은 좌표평면 상에서 꼭짓점의 좌표를 알 때 다각형의 면적을 구할 수 있는 방법입니다. 이따 사용방법을 보면 알겠지만, 구할 때 삼각형의 각 꼭짓점의 좌푯값을 교차하여 곱하는 모습이 신발끈을 묶을 때와 같아 이러한 이름이 붙었습니다. 가우스의 면적 공식이나 사선 공식으로도 불립니다.
이 공식은 두 개 이상의 변들이 서로 교차하는 형태의 다각형이 아니라면, 볼록다각형이든 오목다각형이든 관계없이 적용시킬 수 있습니다. 볼록다각형/오목다각형에 관한 포스팅은 다음에 또 할게요 🙂
직각삼각형의 넓이를 구하라! : 네이버 포스트
[BY LG상남도서관] [풀이] 직각삼각형의 넓이를 구해야 한다고 할 때, 가장 먼저 생각할 수 있는 풀이 …
- Image source: post.naver.com
- Views: 14264
- Publish date: 13 hours ago
- Downloads: 17417
- Likes: 9219
- Dislikes: 9

좋아요 한 사람 보러가기
이전화면으로 가기
#LG사이언스랜드
헤론의 공식 증명 (세 변의 길이로 넓이 구하는 방법)
오늘은 삼각형의 세 번의 길이를 알 때 넓이를 바로 구할 수 있는 공식을 알아볼 거에요. 여러분, 이렇게 세 변의 길이가 주어진 삼각형의 넓이를 어떻게 구하시나요? 당연히 높이가 필요하니까 수선의 발을 그려서 구하면 되겠죠? 밑변을 7이 아닌 6으로 두면, 계산이 좀 쉬워집니다만 어쨌든 꽤 복잡하네요. 그렇지만 오늘 배울 헤론의 공식을 안다면? 이렇게 두 줄만에 간단하게 넓이가 구해진답니다! wow! 어떤가요? 벌써 기대되시죠?ㅎㅎ 그럼 우선 헤론의 공식이 뭔지부터 알아보도록 해요. 헤론의 공식 헤론의 공식은 그리스 시대의 수학자 헤론(Heron)의 이름을 따서 만든 공식입니다. 삼각형에서 세 변의 길이를 알 때, 넓이를 구할 수 있는 공식이죠. 증명은 중2,3때 배우는 피타고라스의 정리와 곱셈공식만 사..
- Image source: ladyang86.tistory.com
- Views: 64395
- Publish date: 4 hours ago
- Downloads: 44280
- Likes: 8691
- Dislikes: 5

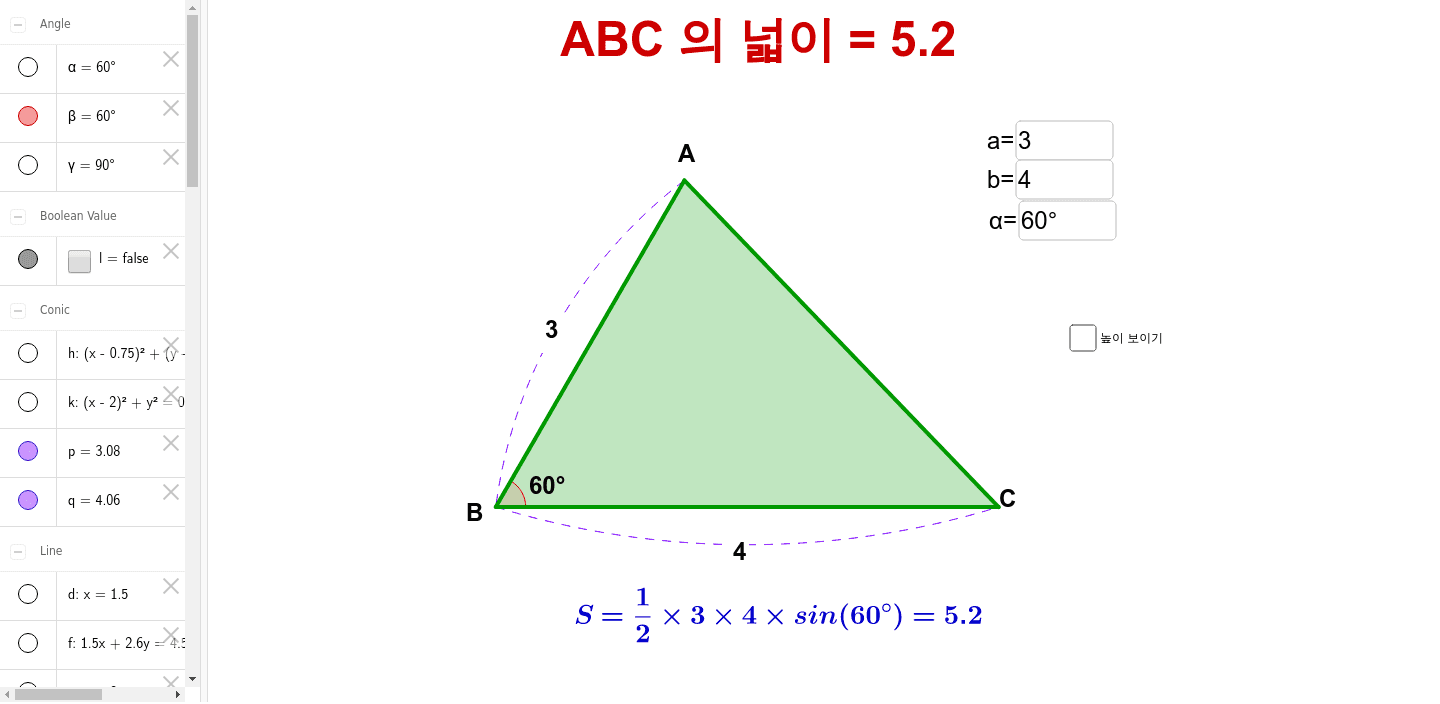
[삼각비] 특수각 사인, 코사인, 탄젠트 15º, 75º, 22.5º, 67.5º
[삼각비] 특수각 사인, 코사인, 탄젠트 15º, 75º, 22.5º, 67.5º [이차방정식 활용] 정오각형과 황금비 (황금삼각형, 사각형)삼각형의 넓이 – GeoGebra
- Image source: www.geogebra.org
- Views: 22445
- Publish date: 16 hours ago
- Downloads: 61848
- Likes: 6026
- Dislikes: 9
George W. Hart 작품 관찰하기
삼각함수(사인, 코사인) 그래프 퀴즈
y=ax그래프에서 a값에 따른 변화
중2 2학기기말고사대비 필수유형정리 높이가 같은 삼각형의 넓이의 비+닮음 삼각형의 내각의 이등분선 공식 : 네이버 블로그
중2 #2학기기말고사대비 필수유형정리높이가같은 삼각형의 넓이의 비 닮음 삼각형의 내각의 이등분선#여러…
- Image source: m.blog.naver.com
- Views: 78253
- Publish date: 42 minute ago
- Downloads: 104655
- Likes: 9530
- Dislikes: 6
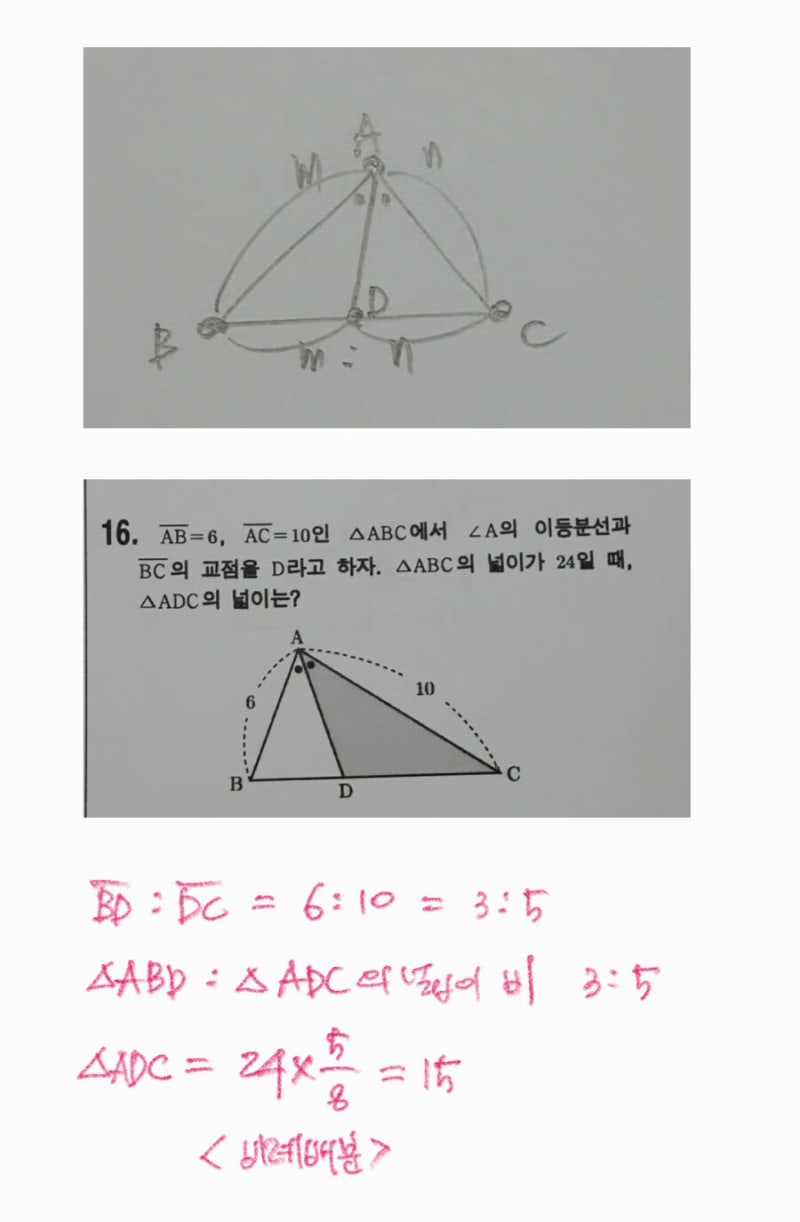
중2 시험대비 삼각형의 무게중심#중2 2학기 기말고사대비용 #무게중심 을 이용하여 답을 구하는 문제는 시…
중2 2학기기말고사대비 필수유형정리 높이가 같은 삼각형의 넓이의 비+닮음 삼각형의 내각의 이등분선 공식
수학 – 초등 4-1 – 삼각형- 오누이
- Image source: onuii.com
- Views: 71745
- Publish date: 21 minute ago
- Downloads: 47283
- Likes: 4636
- Dislikes: 7

넓이는 높이×밑변이므로, 높이는 넓이÷밑변이 돼요!
삼각형의 높이를 구하는 식을 모르겠어요..
2021.09.12 17:54:53
삼각형의 넓이 공식 및 증명하기
개요 모든 삼각형은 두 변의 길이와 그 사이 각의 크기만 알면 넓이를 구할 수 있고 공식화하여 표현할 수 있다. 삼각형의 넓이를 구하는 법을 알아보자. 공식 아래와 같은 삼각형을 가정해보자. 두 변의 길이와 각도를 알 때 삼각형의 넓이는 다음과 같이 표현할 수 있다. 왜 이런 공식이 나오는 걸까? 유도 및 증명 아주 간단하다. 우선 삼각형의 넓이는 밑면의 길이 X 높이 / 2 라는 것을 다들 알고 있을 것이다. 위의 삼각형에서 수직으로 선을 하나 그어보자. 이 삼각형에서 밑면의 길이는 b가 될 것이고 높이 h는 삼각함수 법칙에 의하여 아래와 같이 표현할 수 있다. 밑면의 길이 : b 높이 : asinB 로 표현되기 때문에 삼각형의 넓이는 밑면의 길이 X 높이 / 2 를 적용하면 이렇게 공식이 만들어지는 ..
- Image source: houseofj.tistory.com
- Views: 4560
- Publish date: 5 hours ago
- Downloads: 18645
- Likes: 1270
- Dislikes: 9
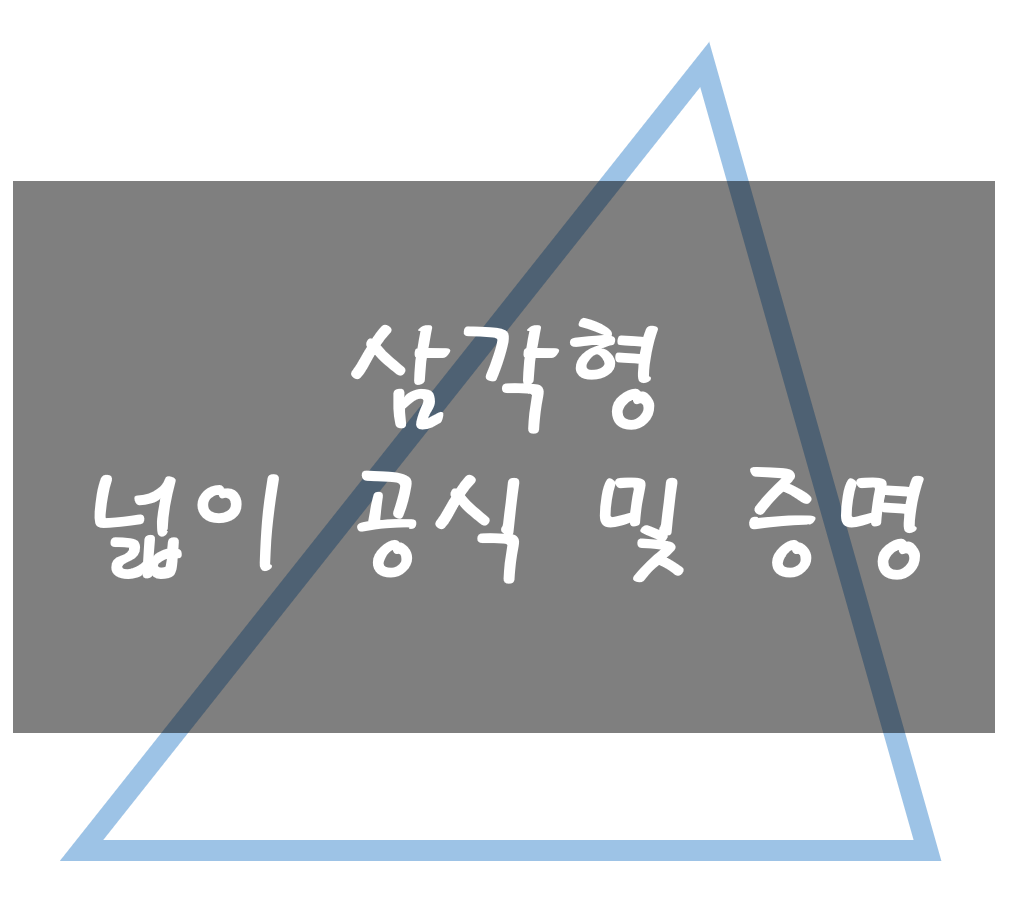
모든 삼각형은 두 변의 길이와 그 사이 각의 크기만 알면 넓이를 구할 수 있고 공식화하여 표현할 수 있다. 삼각형의 넓이를 구하는 법을 알아보자.
이 삼각형에서 밑면의 길이는 b가 될 것이고 높이 h는 삼각함수 법칙에 의하여 아래와 같이 표현할 수 있다.
우선 삼각형의 넓이는 밑면의 길이 X 높이 / 2 라는 것을 다들 알고 있을 것이다.
삼각형의 넓이 구하는 법 – wikiHow
흔히 삼각형의 넓이는 밑변에 높이를 곱해 2로 나눠서 구한다. 물론 삼각형의 넓이를 구하는 공식은 여러 가지가 있으나 이는 결국 문제에서 주어지는 정보에 따라 달라진다. 삼각형의 변의 길이와 각도만 주어졌거나, 심지어 높이를 모른다 하더라도 충분히 넓이를 구할 수 있다. 삼각형의 밑변과 높이 찾기. 밑변은 삼각형의 한 변의 길이와 같다. 높이는 밑변에서 마주보는 꼭짓점까지 수직인 선을 그었을 때 그 선분의 길이를 뜻한다….
- Image source: ko.wikihow.com
- Views: 14088
- Publish date: 46 minute ago
- Downloads: 65109
- Likes: 1834
- Dislikes: 5

{“smallUrl”:”https:\/\/www.wikihow.com\/images_en\/thumb\/1\/12\/Calculate-the-Area-of-a-Triangle-Step-10-Version-5.jpg\/v4-460px-Calculate-the-Area-of-a-Triangle-Step-10-Version-5.jpg”,”bigUrl”:”https:\/\/www.wikihow.com\/images\/thumb\/1\/12\/Calculate-the-Area-of-a-Triangle-Step-10-Version-5.jpg\/v4-728px-Calculate-the-Area-of-a-Triangle-Step-10-Version-5.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:728,”bigHeight”:546,”licensing”:”
{“smallUrl”:”https:\/\/www.wikihow.com\/images_en\/thumb\/b\/b4\/Calculate-the-Area-of-a-Triangle-Step-11-Version-5.jpg\/v4-460px-Calculate-the-Area-of-a-Triangle-Step-11-Version-5.jpg”,”bigUrl”:”https:\/\/www.wikihow.com\/images\/thumb\/b\/b4\/Calculate-the-Area-of-a-Triangle-Step-11-Version-5.jpg\/v4-728px-Calculate-the-Area-of-a-Triangle-Step-11-Version-5.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:728,”bigHeight”:546,”licensing”:”
{“smallUrl”:”https:\/\/www.wikihow.com\/images_en\/thumb\/3\/3f\/Calculate-the-Area-of-a-Triangle-Step-12-Version-5.jpg\/v4-460px-Calculate-the-Area-of-a-Triangle-Step-12-Version-5.jpg”,”bigUrl”:”https:\/\/www.wikihow.com\/images\/thumb\/3\/3f\/Calculate-the-Area-of-a-Triangle-Step-12-Version-5.jpg\/v4-728px-Calculate-the-Area-of-a-Triangle-Step-12-Version-5.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:728,”bigHeight”:546,”licensing”:”
수학 – 수1 – 삼각함수- 오누이
- Image source: onuii.com
- Views: 84306
- Publish date: 1 hours ago
- Downloads: 10888
- Likes: 5734
- Dislikes: 3

문제에서 제시한 삼각형의 세 변의 길이는 5, 6, 7입니다. 헤론의 공식을 보다 편리하게 사용하기 위해서 우리는 s라는 값을 설정하는데요, 삼각형의 둘레의 길이의 절반, 즉, 삼각형의 세 변의 길이의 합을 2로 나눠준 값입니다. 문제의 풀이에서도 s값을 먼저 잡아준 것을 확인할 수 있죠.
헤론의 공식은 삼각형의 세 변의 길이를 알 때, 그 세 변의 길이만으로 삼각형의 넓이를 구하는 공식이에요. 현재 교육과정에는 없어서 학교에서는 아마 가르쳐주지 않을 거에요.
즉, 어떤 삼각형의 세 변의 길이가 a, b, c일 때 그 삼각형의 넓이는 루트{s(s-a)(s-b)(s-c)} 라는 것이 바로 헤론의 공식입니다.
삼각형의 넓이가 최소가 되는 조건 구하기 문제
(문제) 두 반직선 사이에 정점 P가 있다. P를 지나는 직선과 반직선으로 이루어진 삼각형의 넓이가 최소가 되는 조건을 구하여라. 참고: 둘레의 길이가 최소가 되는 조건 https://mathpeak.tistory.com/47 지중상 34단원 연습문제 9번 풀이 (문제) 각 AOB 내부에 점 P가 있고, 점 P를 지나는직선이 반직선 OA, OB와 각각 C, D에서 만난다고 할 때, 삼각형 OCD의 둘레의 최솟값을 구하여라. (문제) 점 P는 정해진 각 AOB의 내부에 있는 정점이다. 각 A.. mathpeak.tistory.com (풀이 1) (풀이 2) (풀이 3) – 산술기하부등식을 이용한 풀이 ★ P가 변 CP의 중점이 되도록 작도하는 문제 https://mathpeak.tistory.com/408..
- Image source: mathpeak.tistory.com
- Views: 27400
- Publish date: 23 minute ago
- Downloads: 23218
- Likes: 3228
- Dislikes: 6

부분분수의 합으로 표현하는 방법 Heaviside method
부분분수의 합으로 표현하는 방법 Heaviside method
https://mathpeak.tistory.com/408
도형의 넓이 : WHY브러리
제 13회 창의력 글쓰기 대회 수학일기 우수상와이즈만 영재교육 대전송촌센터 5학년 이은서이번에는 다양한 도형의 넓이를 구하는 방법에 대해 배웠다.직사각형의 넓이가 《가로x세로》인것은 이미 알고 있었다. 먼저, 평해사변형의 넓이를 알아보자.평행사변형은 두쌍이 평행한 사각형이고 마주보는 변의 길이가 같다.평행사변형을 그림고 ㅏ같이 잘라서 붙이면 직사각형 모양으로 만들수 있다.그러므로 넓이는 《밑변x높이》이다.두번째로 삼각형 넓이를 구하는 방법을 알아보자.그림과 같이 삼각형을 2개 이어 붙이면 평행사면형이 된다.그래서 넓이는 평행사변형을 이용해서 구할 수 있다.만들어진 평행사변형의 절반이므로 삼각형의 넓이는 《밑변x높이÷2》가 된다.세번째로 사다리꼴 넓이를 구하는 방법에 대해 알아보자사다리꼴은 한쌍의 변이 평행한 사각형이다. 사다리꼴 2개를 붙이면 평행사변형이된다.만들어진 평행사변형의 밑변이 사다리꼴의 "아랫변+윗변"이므로 사다리꼴의 넓이는 《(윗변+아랫변)×높이÷2》가 된다.마지막으로 마름모 넓이를 구하는 방법을 알아보자.마름모는 네변의 길이가 같은 사각형이다. 그림과 같은 직사각형은마름모 넓이의 2배인것을 알 수 있다.직사각형 넓이의 절반이니까 마름모의 넓이는《한대각선×다른대각선÷2》가 된다.그런데 위에 ☆정리☆ 같은 도형이 아닐때는 넓이를 어떻게 구할까?색칠된 부분의 넓이는 위의 공식으로는 풀 수 없다. 그래서 삼각형을 이용해 넓이를 구할 것이다.큰 삼각형을 이용해 넓이를 구할 것이다.큰 삼각형의 넓이는 (6+4)×(9+4)÷2가 될것이다.130÷2=65 큰 삼각형의 넓이는 65이다.작은 삼각형의 넓이는 4×9÷2=18, 큰 삼각형의 넓이어서 작은 삼각형의 넓이를 빼주면 된다.즉, 65-18-47이 된다.나는 이번 단원에서 직사각형이 아닌 다른 도형의 넓이를 구할 수 있게 되어 좋았다. 그리고 공식만 외운게 아니라그 이유도 알게되어 뿌듯했다. 앞으로는 넓이문제를 풀때 좀 더 쉽게 구할 수 있을 것 같다.[심사평]이은서 학생은 <도형의 넓이>에서 삼각형과 사각형의 넓이를 구하는 방법의 원리를 탐구하고 일기를 작성하였습니다.이은서 학생은 평행사변형, 삼각형, 사다리꼴, 마름모 등 다양한 사각형과 삼각형의 넓이를 구하는 방법의원리를 그림을 이용하여 이해하기 쉽게 정리하였습니다. 단순히 넓이를 구하는 공식을 도출하는 것에서 나아가 복잡한 형태의 도형이 주어졌을 때 학습한 내용을 적용하여 도형의 넓이를 구하는 방법까지 수학일기에 잘 정리되어 있습니다. 단순히 공식을 외워 문제를 해결하는 것이 아닌 공식을 도출하는 원리를 이해하게 된 것에 뿌듯함을 느끼는 이은서 학생의 모습에서 수학자 못지 않는 탐구심을 볼 수 있었습니다.지금과 같이 수학적 원리에 대한 흥미와 호기심을 바탕으로 깊이 있는 탐구를 하고, 나아가 더 알고 싶은 내용까지 생각하고 탐구해 본다면 지금보다 더욱 성장하는 이은서 학생이 될 것입니다.[ 작품 원본 보기 ▽ ][위 작품은 와이즈만 영재교육과 와이키즈에서 개최하는 '수학・과학 창의력 글쓰기 대회'에 출품된 작품입니다.]#와이즈만 #와이키즈 #창의력글쓰기대회 #띵작 #수상작 #고학년 #우수상 #수학일기 #와이즈만수학일기 #5학년 #초등수학 #와이즈만수학 #와이즈만수학수업 #와이즈만5학년 #5학년수학 #도형 #CT플러스 #삼각형 #사각형 #평행사변형 #사다리꼴 #마름모
- Image source: whybrary.mindalive.co.kr
- Views: 107702
- Publish date: 23 hours ago
- Downloads: 86168
- Likes: 1043
- Dislikes: 9
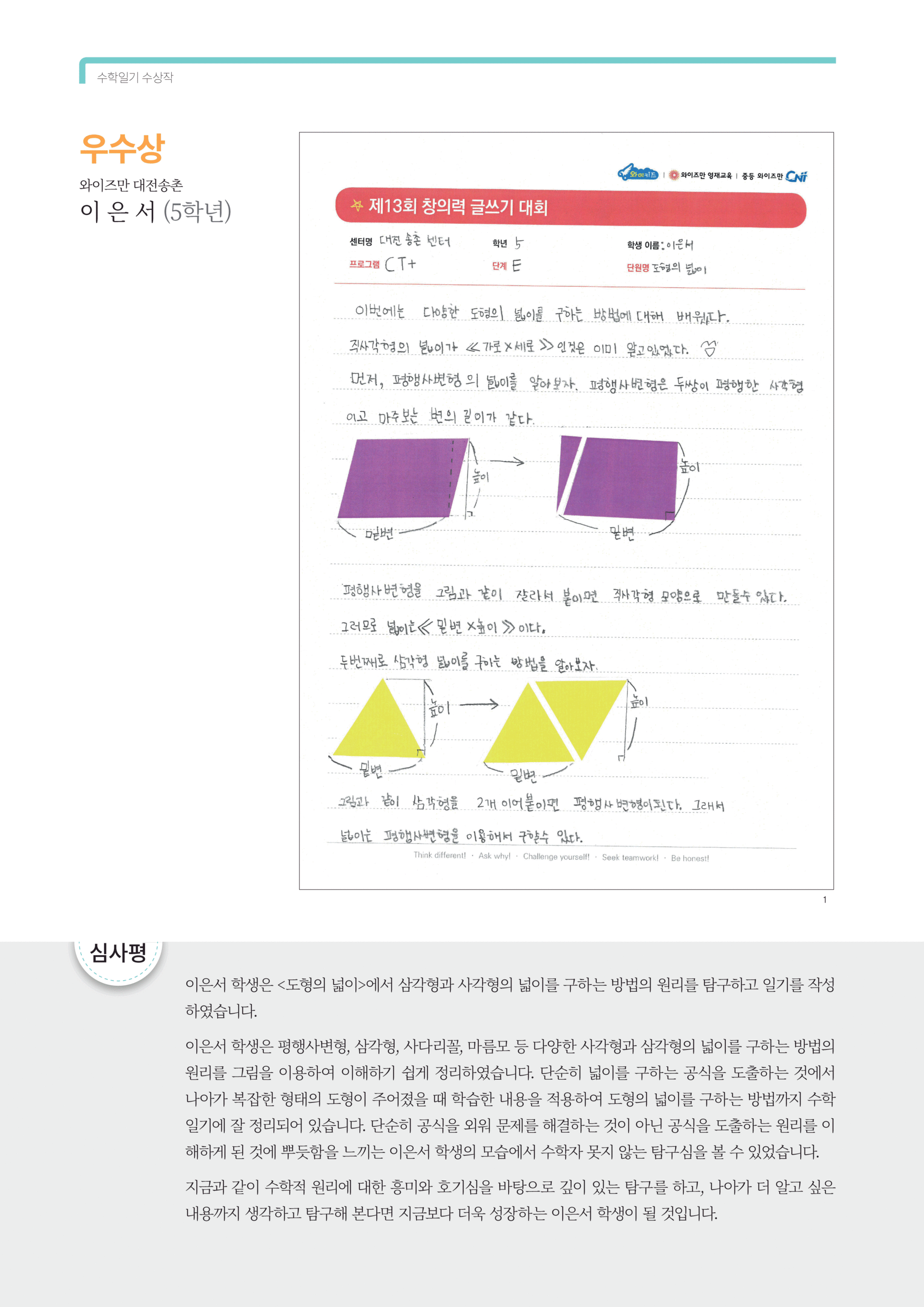
이은서 학생은 평행사변형, 삼각형, 사다리꼴, 마름모 등 다양한 사각형과 삼각형의 넓이를 구하는 방법의원리를 그림을 이용하여 이해하기 쉽게 정리하였습니다. 단순히 넓이를 구하는 공식을 도출하는 것에서 나아가 복잡한 형태의 도형이 주어졌을 때 학습한 내용을 적용하여 도형의 넓이를 구하는 방법까지 수학일기에 잘 정리되어 있습니다. 단순히 공식을 외워 문제를 해결하는 것이 아닌 공식을 도출하는 원리를 이해하게 된 것에 뿌듯함을 느끼는 이은서 학생의 모습에서 수학자 못지 않는 탐구심을 볼 수 있었습니다.
#와이즈만 #와이키즈 #창의력글쓰기대회 #띵작 #수상작 #고학년 #우수상 #수학일기 #와이즈만수학일기 #5학년 #초등수학 #와이즈만수학 #와이즈만수학수업 #와이즈만5학년 #5학년수학 #도형 #CT플러스 #삼각형 #사각형 #평행사변형 #사다리꼴 #마름모
지금과 같이 수학적 원리에 대한 흥미와 호기심을 바탕으로 깊이 있는 탐구를 하고, 나아가 더 알고 싶은 내용까지 생각하고 탐구해 본다면 지금보다 더욱 성장하는 이은서 학생이 될 것입니다.
측정 : 넓이란 무엇인가. – ppt download
4.1 서론 이 장에서 우리는 날마다 다양한 분야에서 사용되는 넓이와 부피에 대한 개념들을 기하학, 대수학, 삼각함수, 확률, 그리고 기초미적분학과 연결하여 주의 깊게 살펴본다.
- Image source: slidesplayer.org
- Views: 38018
- Publish date: 60 minute ago
- Downloads: 102330
- Likes: 3305
- Dislikes: 1
원의 둘레는 2πr이다. 그것을 어떻게 알 수 있을까? 답을 알면 놀랄지도 모르겠다. 수 천년 전에 원의 둘레 C와 원의 지름 d의 비율이 원의 크기에 상관 없이 항상 같다는 사실이 발견되었다. 이 비율은 3을 약간 넘었다. 이것은 실험에 의해 반복적으로 입증된 발견이었다. 형식적인 증명은 없었다. 그래서 이것은 원의 둘레의 성질에 대하여 받아들여진 사실이었다. 그것은 관찰에 기반한 공리였다. 어쩌면 당신은 ‘그래도 증명이 필요하지 않을까?’ 라고 불안해 할 지도 모르겠다. 그래서 이것이 참이라고 당신을 안심시키기 위해 몇 가지 보강을 할 것이다.
그래서 우리는 관찰에 기반하여 원의 둘레와 지름의 길이의 비가 항상 같다는 사실을 받아들일 것이다. 이 비율의 이름이 무엇일까? 영국의 수학자 William Oughtred는 1647년에 쓴 책 Clavis Mathematicae(The Key to Mathematics)에서 원의 둘레(periphery)와 지름의 비율을 나타낼 기호가 있으면 좋겠다고 생각했다. 그런데 수학자들은 수학 기호를 표현할 때 그리스 문자를 사용하는 습관이 있기 때문에, 그는 π를 사용했다. 이는 π가 둘레를 뜻하는 periphery에서 유래했다는 것을 상기시킨다.
We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!
비디오 삼각형의 넓이 구하는 공식 삼각형의 넓이 구하는 방법 (초등수학)
- Source: Youtube
- Views: 36194
- Date: 47 minute ago
- Download: 79519
- Likes: 6724
- Dislikes: 2
주제에 대한 관련 정보 삼각형의 넓이 구하는 공식
Bing에서 삼각형의 넓이 구하는 공식 주제에 대한 최신 정보를 볼 수 있습니다.
초등 삼각형의 넓이 공식
삼각형 넓이 공식 모음
삼각형의 넓이 구하는 방법 5학년
직각삼각형 넓이 구하는 방법
초등학교 삼각형 넓이
이등변삼각형 넓이 공식
삼각형의 넓이 sin
삼각형 넓이 공식 sin
주제에 대한 기사 보기를 마쳤습니다 삼각형의 넓이 구하는 공식. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.
초등 삼각형의 넓이 공식
삼각형 넓이 공식 모음
삼각형의 넓이 구하는 방법 5학년
직각삼각형 넓이 구하는 방법
초등학교 삼각형 넓이
이등변삼각형 넓이 공식
삼각형의 넓이 sin
삼각형 넓이 공식 sin