톱 104 훅 의 법칙 새로운 업데이트 72 분 전

by

훅의 법칙 나무위키

훅의 법칙 텐서

훅의 법칙 탄성계수

훅의 법칙 유도

후크 법칙

용수철 상수

훅의 법칙 문제

탄성력 공식

주제에 대한 기사를 찾고 있습니까 “훅 의 법칙“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: 974 사진을 다운로드할 수 있는 최고의 웹사이트. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.

이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.

컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.

후크 법칙은 고체에 힘을 가해 변형시킬 때, 힘이 어떤 크기를 넘지 않으면 고체의 변형된 정도는 힘의 크기에 정비례한다는 법칙으로, 고체역학의 기본 법칙 중의 하나이다. 이 법칙이 성립하는 한계를 넘어서면 탄성의 한계를 넘게 되는 것이고, 물체는 탄성을 잃고 영구적으로 변형되게 된다.

훅 의 법칙 주제와 관련된 상위 64 이미지

주제 훅 의 법칙 와 관련된 44 개의 이미지가 있습니다.

훅의 법칙 – 위키백과, 우리 모두의 백과사전

  • Image source: ko.wikipedia.org
  • Views: 103413
  • Publish date: 14 minute ago
  • Downloads: 6128
  • Likes: 5402
  • Dislikes: 4
훅의 법칙 - 위키백과, 우리 모두의 백과사전
훅의 법칙 – 위키백과, 우리 모두의 백과사전

. (Walter Lewin (1 October 1999). Hooke’s Law, Simple Harmonic Oscillator. MIT Course 8.01: Classical Mechanics, Lecture 10. (ogg) (videotape) (in English). Cambridge, MA USA: MIT OCW. Event occurs at 1:21–10:10. Retrieved 23 December 2010. “…arguably the most important equation in all of Physics.”)

. (Walter Lewin (1 October 1999). Hooke’s Law, Simple Harmonic Oscillator. MIT Course 8.01: Classical Mechanics, Lecture 10. (ogg) (videotape) (in English). Cambridge, MA USA: MIT OCW. Event occurs at 10:10–16:33. Retrieved 23 December 2010. “)

로 변형 상태를 나타내기로 한다. x > 0 이면 늘어난 것이고, x < 0 이면 줄어든 것이다. 용수철 길이의 변화가 x 일 때의 복원력을 F 로 하자. 힘이 오른쪽 방향이면 F > 0 이고, 왼쪽 방향이면 F < 0이라 한다. 이 때, 훅의 법칙은 다음과 같이 나타낼 수 있다.

훅의 법칙 – 위키백과, 우리 모두의 백과사전

  • Image source: ko.wikipedia.org
  • Views: 30754
  • Publish date: 22 hours ago
  • Downloads: 83579
  • Likes: 7203
  • Dislikes: 6
훅의 법칙 - 위키백과, 우리 모두의 백과사전
훅의 법칙 – 위키백과, 우리 모두의 백과사전

. (Walter Lewin (1 October 1999). Hooke’s Law, Simple Harmonic Oscillator. MIT Course 8.01: Classical Mechanics, Lecture 10. (ogg) (videotape) (in English). Cambridge, MA USA: MIT OCW. Event occurs at 1:21–10:10. Retrieved 23 December 2010. “…arguably the most important equation in all of Physics.”)

. (Walter Lewin (1 October 1999). Hooke’s Law, Simple Harmonic Oscillator. MIT Course 8.01: Classical Mechanics, Lecture 10. (ogg) (videotape) (in English). Cambridge, MA USA: MIT OCW. Event occurs at 10:10–16:33. Retrieved 23 December 2010. “)

로 변형 상태를 나타내기로 한다. x > 0 이면 늘어난 것이고, x < 0 이면 줄어든 것이다. 용수철 길이의 변화가 x 일 때의 복원력을 F 로 하자. 힘이 오른쪽 방향이면 F > 0 이고, 왼쪽 방향이면 F < 0이라 한다. 이 때, 훅의 법칙은 다음과 같이 나타낼 수 있다.

File:Hooke’s Law wikipedia.png – Wikimedia Commons

  • Image source: commons.wikimedia.org
  • Views: 52069
  • Publish date: 22 hours ago
  • Downloads: 28922
  • Likes: 4283
  • Dislikes: 7
File:Hooke'S Law Wikipedia.Png - Wikimedia Commons
File:Hooke’S Law Wikipedia.Png – Wikimedia Commons

This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.

{{파일 정보 |설명= 훅의 법칙을 그림으로 나타낸 것이다. |출처= 직접 제작 |날짜= 2012.04.24 |만든이= 직접 제작 |저작권= 직접 제작 |기타= http://ko.wikipedia.org/wiki/훅의_법칙 을 참조하였습니다. }}

https://commons.wikimedia.org/w/index.php?title=File:Hooke%27s_Law_wikipedia.png&oldid=630087657

훅의 법칙 뜻: 탄성체의 일그러짐은 변형력에 비례한다는 법칙. 변형력이 어떤 크기를 넘지 않는 한 모든 고

훅의 법칙: 탄성체의 일그러짐은 변형력에 비례한다는 법칙. 변형력이 어떤 크기를 넘지 않는 한 모든 고체에 대하여 성립한다. 영국의 물리학자 훅이 발견하였다. (어휘 혼종어 물리 )

  • Image source: wordrow.kr
  • Views: 22829
  • Publish date: 40 minute ago
  • Downloads: 91982
  • Likes: 7163
  • Dislikes: 10
훅의 법칙 뜻: 탄성체의 일그러짐은 변형력에 비례한다는 법칙. 변형력이 어떤 크기를 넘지 않는 한 모든 고
훅의 법칙 뜻: 탄성체의 일그러짐은 변형력에 비례한다는 법칙. 변형력이 어떤 크기를 넘지 않는 한 모든 고

흑화 법칙, 현지성의 원칙, 통화 정책 준칙, 개별 보상의 원칙, 상호 호혜 원칙, 생체 원칙, 다수반칙, 질소 규칙, 베버의 법칙, 상사 생육의 법칙, 하트위크 법칙, 뉴턴의 냉각 법칙, 불이익 변경 금지 원칙, 불규칙, 직접 운송 원칙, 추심 통일 규칙, 동등 희생의 원칙, 비례성 원칙, 자산 평가 원칙, 신칙, 탄력성의 원칙, 연산자 결합 법칙, 국제 협력의 원칙, 오차 법칙, 선택 법칙, 경험 법칙, 국적 자유의 원칙, 방사 휘도 보존 법칙, 나역등칙, 윈드 시어 지수 법칙, 다수결의 원칙, 어벡 법칙, 관리 원칙, 비용 수익 대응의 원칙, 무관용 원칙, ㅂ 받침 변칙, 배분 법칙, 수요의 법칙, 스케줄링 보존 법칙, 일관된 반대 국가의 원칙, 수익자 부담 원칙, 최소 비용의 원칙, 제일 코싸인 법칙, 플레밍의 오른손 법칙, 플랑크의 법칙, 공개 재판의 원칙, 우 변칙, ㄷ 변칙, 질량 작용의 법칙, 구절 구조 규칙, 항해 규칙, 회로 법칙, 연역적 추론 규칙, 비용 체감의 법칙, 께름칙, 피트의 법칙, 뉴턴의 제삼 법칙, 확률의 덧셈 법칙, 광화학 당량의 법칙, 심장의 법칙 …

칙, 칙가드, 칙가라미범, 칙간, 칙갈맞다, 칙고, 칙교, 칙교하다, 칙구소, 칙굴, 칙권, 칙권하다, 칙단, 칙단하다, 칙답, 칙답하다, 칙령, 칙례, 칙릿, 칙명, 칙문, 칙문하다, 칙바귀, 칙백나무, 칙백낭구, 칙범, 칙봉, 칙사, 칙사 대접, 칙사등록, 칙사증급록, 칙살, 칙살맞다, 칙살부리다, 칙살스럽다, 칙살스레, 칙살하다, 칙상, 칙서, 칙선, 칙선되다, 칙선하다, 칙수, 칙수백장청규, 칙시깐, 칙액, 칙어, 칙어하다, 칙유, 칙유하다, 칙은덕하다, 칙은하다, 칙이다, 칙임, 칙임관, 칙임하다, 칙재, 칙재하다, 칙제, 칙조 …

녹아웃 훅, 쇼트 훅, 버튼 훅, 피시 훅, 스카이 훅, 리드 훅, 셰퍼드 훅, 진훅, 스카이훅, 힐 훅, 갈고리 훅, 넉아웃 훅, 오프훅, 펠리컨 훅, 어저스터블 훅, 핸드 라인 훅, 도체 인상 훅, 섬유 훅, 러시안 훅, 라이트 훅, 스테이 훅, 그래브훅, 퀵 훅, 레이우엔훅, 니들 훅, 스위치 훅, 레프트 훅, 훅, 온훅, 더크 훅, 피피 훅, 캠 훅, 유지 보수 훅, 미트 훅, 훅훅, 게훅, 교환 훅 …

[고급물리학] 뉴턴 운동 법칙과 여러 가지 힘

2022.04.05 – [2022 고급물리학] – [고급물리학] 힘과 운동(벡터, 가속도, 포물선 운동, 등속 원운동) [고급물리학] 힘과 운동(벡터, 가속도, 포물선 운동, 등속 원운동) 학습 목표 물리량을 벡터와 스칼라로 구분하고, 벡터의 연산(내적, 외적)을 할 수 있다. 가속도의 의미를 이해하고 미분을 이용하여 표현할 수 있으며, 등가속도 운동에서 위치, 속도, 가속도 사 gooseskin.tistory.com 학습 목표 힘과 운동의 관계를 다루는 동역학에 대하여 설명할 수 있다. 동역학의 핵심 내용인 뉴턴의 운동 법칙들의 의미를 설명할 수 있다. 여러 가지 힘이 작용하는 경우의 물리량을 구하는 예에서 미분이 포함된 운동 방정식을 해결할 수 있다. 물리학 전개도 1. 뉴턴 운동 1법칙, 관성 법칙..

  • Image source: gooseskin.tistory.com
  • Views: 77119
  • Publish date: 24 minute ago
  • Downloads: 64652
  • Likes: 4065
  • Dislikes: 4
고급물리학] 뉴턴 운동 법칙과 여러 가지 힘
고급물리학] 뉴턴 운동 법칙과 여러 가지 힘

트럭 위의 사람이 공을 위로 던지고 있다. 공이 손을 떠나는 순간, 트럭 안의 사람과 트럭 밖에서 정지해 있는 사람이 보는 공의 운동 궤적은 서로 다르다. 그러나 공이 바닥에 떨어지게 되는 결과, 바닥에 닿는 공의 속력과 바닥에 닿는 데 걸린 시간은 두 사람에게 똑같이 관찰된다. 왜냐면 이 물체에게 중력이 작용한다는 사실과 물체에 작용하는 힘에 의해 속도가 변화하는 경향은 두 사람에게 동일하기 때문이다. 이처럼 동일한 물리 법칙이 적용되는 두 사람은 각각 정지해있고, 등속 운동을 하고 있으니 이러한 계를 기준계로 설정하고 이를 ‘관성계’라 하는 것이다.

⑦다이빙 선수가 낙하할 때 지구의 중력이 선수를 끌어당기며 지구 중심 방향으로 가속시킨다. 동시에 다이빙 선수도 같은 크기의 힘으로 지구를 끌어당긴다.(지구의 질량이 다이빙 선수의 질량에 비해 매우 커서 같은 크기의 힘이 작용해도 지구의 가속도는 0에 가깝다. 따라서 지구는 힘을 받지 않는 것처럼 보인다.)

물체의 속도, 가속도는 관찰자에 따라 다르게 측정되므로 표준이 될만한 기준계가 필요하다. 그 기준계를 ‘관성계’라고 한다. 관성계에 대해 상대적으로 등속 운동하거나 정지한 좌표계 모두 관성계가 된다. 이러한 관성계에 있는 물체에 아무런 힘도 작용하지 않을 때, 그 물체는 정지해 있거나 등속도 운동을 한다.

[Oscillation] 1차원에서의 훅의 법칙(Hooke’s Law)과 조화 단진자 (Harmonic Simple Oscillation) :: Crush on Study

우리가 배우는 물리에서는 보존장이 크게 3가지로 있습니다. 중력장, 전기장 그리고 용수철 진자운동입니다. 그렇기 때문에 Oscillation이라고 따로 학문이 존재하는데 이는 광학을 배울 때도 많이 중요한 개념으로 작용합니다. 오늘부터 포스팅할 오실레이션은 먼저 1차원에서부터 시작하도록 하겠습니다. ▶ 훅의 법칙 훅의 법칙은 1차원으로 표현했을 때, F(x)=-kx라는 공식을 가집니다. 여기서 x는 델타를 붙여주면 좀 더 정확하구요. Δx는 거리의 변화량을 뜻하고 k는 용수철 상수라고 알려져있습니다. 이 k가 정확히 어떻게 나왔는지 한번 보도록 하겠습니다. 용수철 운동에서의 평형점은 원점이라고 가정하겠습니다. 그러면 1차원에서는 x=0인 곳이 평형점이 되겠죠? 훅의 법칙에서 음수가 붙은 이유는 우리가 가..

  • Image source: crush-on-study.tistory.com
  • Views: 27429
  • Publish date: 9 hours ago
  • Downloads: 102552
  • Likes: 5485
  • Dislikes: 10
Oscillation] 1차원에서의 훅의 법칙(Hooke'S Law)과 조화 단진자 (Harmonic Simple Oscillation)
Oscillation] 1차원에서의 훅의 법칙(Hooke’S Law)과 조화 단진자 (Harmonic Simple Oscillation)

작은 입자 내에서의 변위라고 가정한다면 사실상 2계미분부터는 그 값이 매우 작을 것이기 때문에 0으로 근사시켜도 무방합니다. 그래서 남은게 결국 F(x)=x(dF/dx)_0인데요.  그러면 용수철 상수 k가 1계미분의 음수값이 되겠죠?

사실 훅의 법칙은 매우 간단한 원리고, 자연계에서는 매우 복잡하고 어렵게 표현합니다. 선형 진동이 아닐수도 있구요. 그러한 것들은 나중에 다루기로 하고 우리는 일단  제일 쉬운거부터 천천히 가도록 합시다.

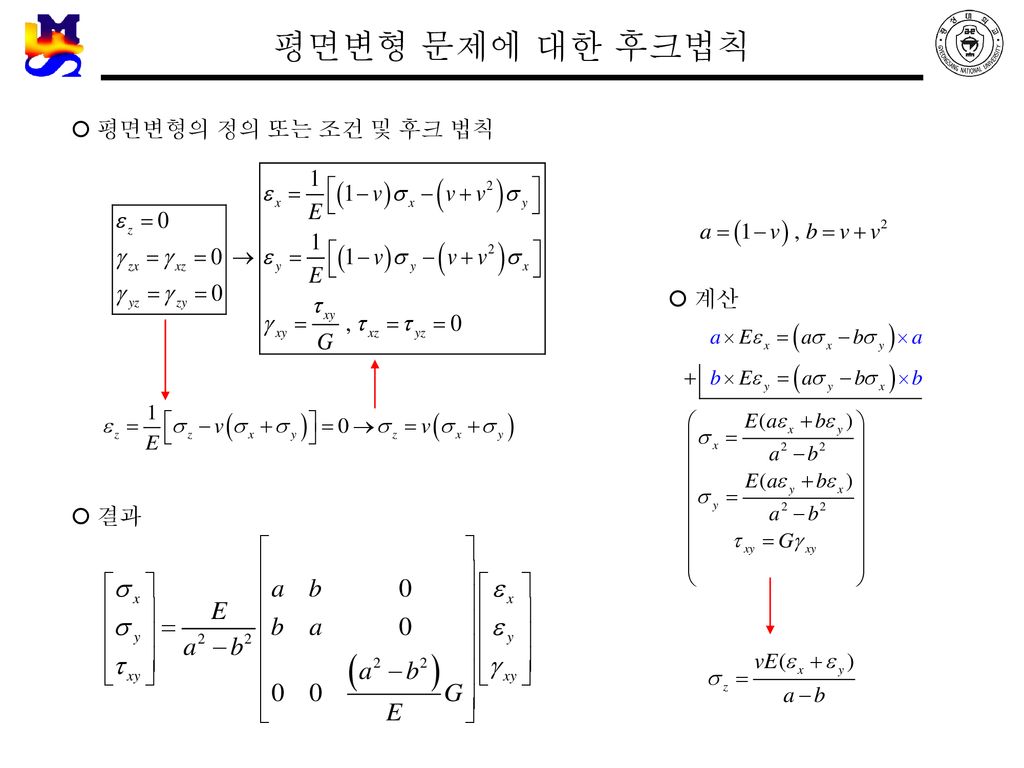
[Oscillation] 1차원에서의 훅의 법칙(Hooke’s Law)과 조화 단진자 (Harmonic Simple Oscillation)

Metal Forming CAE Lab., Gyeongsang National University – ppt download

변형률(Strain) 법선변형률(Normal strain) 전단변형률(Shear strain) 변형률텐서(Strain tensor)

  • Image source: slidesplayer.org
  • Views: 75208
  • Publish date: 23 hours ago
  • Downloads: 73331
  • Likes: 8832
  • Dislikes: 7
Metal Forming Cae Lab., Gyeongsang National University - Ppt Download
Metal Forming Cae Lab., Gyeongsang National University – Ppt Download

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

R-value 박판성형 소성변형률비(Plastic Strain Ratio), R은 인장시편의 폭방향 진변형률과 두께방향 변형률의 비로 표시한다.   압연방향과 0˚방향의 시편으로부터 측정한 소성변형률비(R0)는 이고, 압연방향과 90˚방향의 시편에서 측정한 소성변형률비(R90)는.

5급 승진 후보자 기획보고서 역량평가 대비 교육 안내 (대학교/교육청/중앙부처/지자체 등) 역량평가아카데미 2014년 5급승진을 위한 역량평가 대비를 위해서 다음과 같이 “기획보고서 교육”을 실시하오니 상담후 신청 바랍니다. 모든 기관의 공통 역량평가사항인 “ 사례제시형.

로버트 훅(Robert Hooke, 1635~1703) – ‘훅의 법칙’ 그리고 ‘식물 세포 구조’를 발견한 훅 : 네이버 블로그

&nbsp; &nbsp;현미경의 조명장치를 고안해서 개량한 현미경으로 동식물을 상세하게 관찰하는가 하면, 코르…

  • Image source: m.blog.naver.com
  • Views: 47581
  • Publish date: 2 hours ago
  • Downloads: 49609
  • Likes: 8444
  • Dislikes: 9
로버트 훅(Robert Hooke, 1635~1703) - '훅의 법칙' 그리고 '식물 세포 구조'를 발견한 훅 : 네이버 블로그
로버트 훅(Robert Hooke, 1635~1703) – ‘훅의 법칙’ 그리고 ‘식물 세포 구조’를 발견한 훅 : 네이버 블로그

보일과 훅 그리고 뉴턴이 활동하던 시절은 유럽에 절대 왕정이 성립하여 중앙정부의 관료체계 속으로 혹은 국립 과학 학회 속으로 과학이 편입되었다. 세 과학자는 영국 왕립학회를 중심으로 활동하면서 서로 경쟁하고 교류하였다. 이 시절의 국왕인 제임스 2세는 왕권신수설에 입각한 전제 정치를 하여 영국 의회의 반발을 가져왔다. 의회와 네덜란드의 오렌지 공 윌리엄이 연합하여 제임스 2세를 퇴위시키고 윌리엄 3세로 즉위하였다. 이 사건을 명예혁명이라고 한다. 다음 해(1689)에 발표된 권리장전은 역사적으로 중요한 의미를 갖는다.

권리장전의 내용은 의회의 승인 없이 법률의 정지나 면제, 금전 징수, 상비군의 유지를 할 수 없으며, 의회 안에서의 언론의 자유, 왕위 계승의 순서와 자격 등을 규정했다. 영국의 권리장전은 미국의 독립선언, 버지니아 권리장전, 매사추세츠 권리선언 등에도 영향을 주었고, 이들을 통하여 다시 프랑스 인권선언에도 영향을 끼쳤다. 윌리암 3세는 프랑스의 루이 14세의 유럽지배 실현을 저지하는 데 힘을 기울였다.

6. 일과 에너지에 힘 변위 © 2014 Pearson Education, Inc.. – ppt download

6장의 내용 6.1 일정한 힘이 하는 일 6.2 변하는 힘이 하는 일 6.3 운동 에너지와 일·에너지 원리 6.4 퍼텐셜 에너지 6.5 보존력과 비보존력 6.6 운동 에너지와 운동 에너지 보존 6.7 운동 에너지 보존을 이용한 문제 풀이 6.8 다른 형태의 에너지와 에너지 변환, 에너지 보존 법칙 6.9 소모성 힘을 포함한 에너지 보존과 문제 풀이 6.10 일률 © 2014 Pearson Education, Inc.

  • Image source: slidesplayer.org
  • Views: 83157
  • Publish date: 8 hours ago
  • Downloads: 59056
  • Likes: 7137
  • Dislikes: 3
6. 일과 에너지에 힘 변위 © 2014 Pearson Education, Inc.. - Ppt Download
6. 일과 에너지에 힘 변위 © 2014 Pearson Education, Inc.. – Ppt Download

6.1 일정한 힘이 하는 일 6.2 변하는 힘이 하는 일 6.3 운동 에너지와 일·에너지 원리 6.4 퍼텐셜 에너지 6.5 보존력과 비보존력 6.6 운동 에너지와 운동 에너지 보존 6.7 운동 에너지 보존을 이용한 문제 풀이 6.8 다른 형태의 에너지와 에너지 변환, 에너지 보존 법칙 6.9 소모성 힘을 포함한 에너지 보존과 문제 풀이 6.10 일률

1400 kg인 자동차가 (a) 80 km/h로 일정하게 10°의 언덕(상당히 가파른 언덕)을 올라갈 경우, (b) 평평한 도로에서 다른 차를 추월하기 위해 6.0 s 동안에 90 km/h에서 110 km/h로 가속할 경우에 필요한 일률을 구하라. 차의 움직임을 방해하는 힘은 모두 FR = 700 N이라고 가정한다(그림 6.26).

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

19.일반화된 후크의 법칙1 – 수직응력, 변형률

>>> 일반화된 후크의 법칙1 강의 바로가기

  • Image source: mathmecha.tistory.com
  • Views: 89820
  • Publish date: 18 minute ago
  • Downloads: 106271
  • Likes: 3888
  • Dislikes: 3
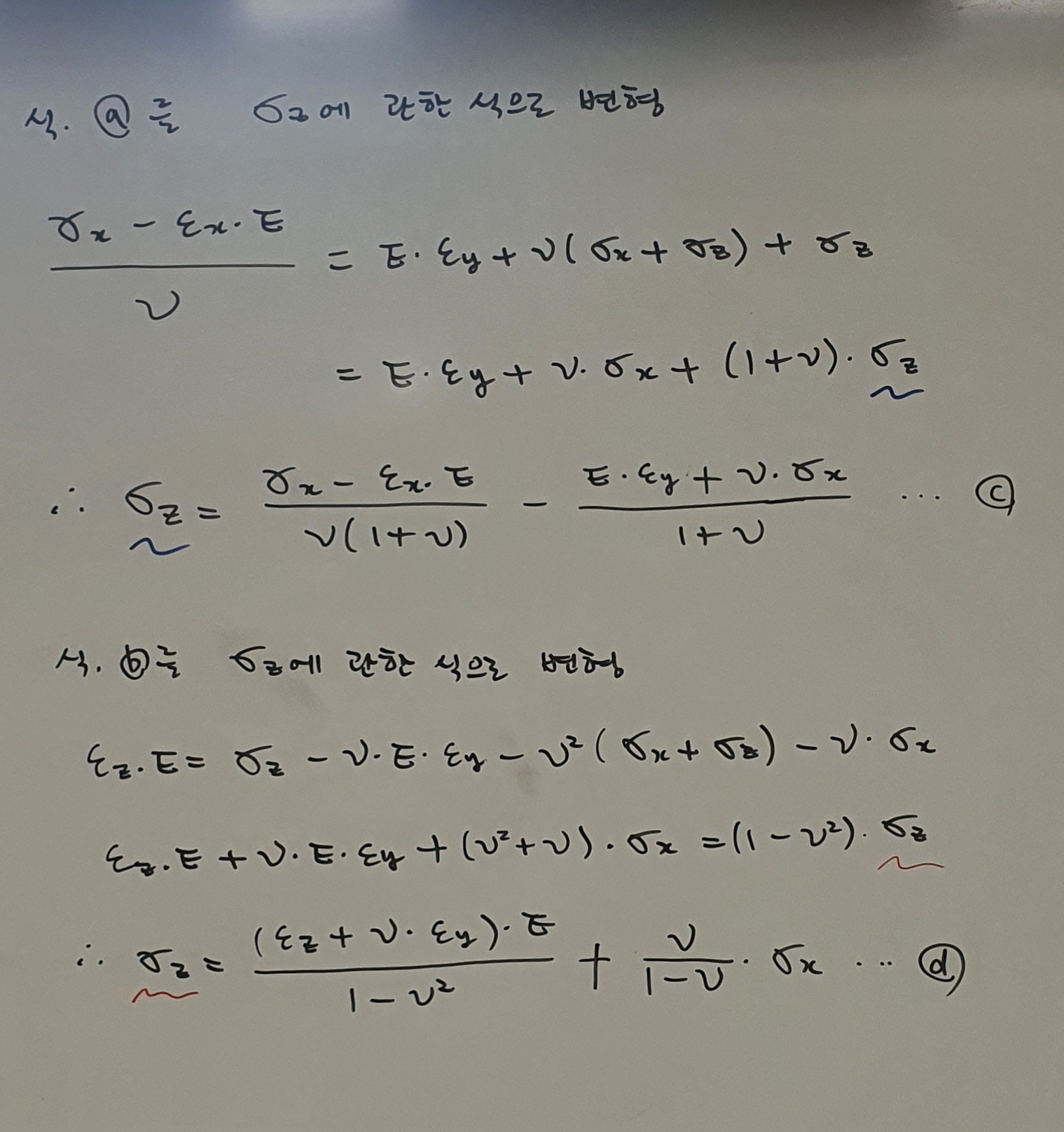
19.일반화된 후크의 법칙1 - 수직응력, 변형률
19.일반화된 후크의 법칙1 – 수직응력, 변형률

한 변의 길이가 dL인 재료의 미소 부분에 2축 수직 응력(σx, σy)이 가해질 때, 각각의 응력은 축방향으로의 변형률(εx)과 수직한 방향으로의 변형률(εy)을 모두 발생시킨다.

아래 그림.2와 같이 변형 전 원래의 미소 부분에 x축 수직응력(σx, 인장)으로 인한 변형이 발생하면

Copyright © 기계공학자 그리고 기계과선배 All Rights Reserved

응력과 변형률 Metal Forming CAE Lab. Department of Mechanical Engineering – ppt download

인장시험, 재료의 거시적 거동 특성

  • Image source: slidesplayer.org
  • Views: 108752
  • Publish date: 11 hours ago
  • Downloads: 17480
  • Likes: 6048
  • Dislikes: 2
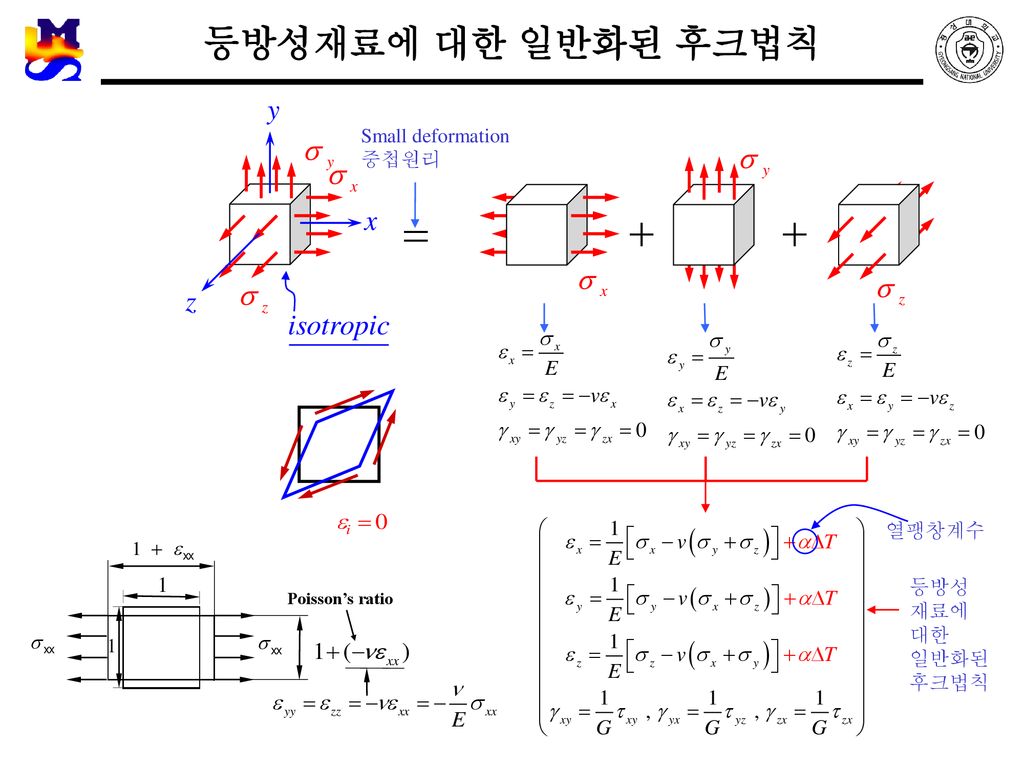
응력과 변형률 Metal Forming Cae Lab. Department Of Mechanical Engineering - Ppt Download
응력과 변형률 Metal Forming Cae Lab. Department Of Mechanical Engineering – Ppt Download

한 면을 x축과 일치시키고, 그림처럼 그 면과 반대편 면에 sigma xx의 응력을 분포시키면, x방향으로는 sigma xx/E(이 분의 시그마 엑스엑스) 만큼의 변형률이 발생하고, y축과 z축으로는 재료의 고유 특성치인 Poisson(포아송)비만큼, 즉 -mu epsilon xx(마이너스 뮤 잎실론 엑스엑스)만큼의 변형률이 발생합니다.

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

1. 2 차원 배열  배열은 동일한 데이터 유형으로 여러 개의 변수를 사용할 경우 같은 이 름으로 지정하여 간편하게 사용할 수 있도록 하는 것으로서 앞에서 1 차원 배열을 공부하였습니다.  2 차원 배열은 바둑판을 생각하면 되며, 1 차원 배열에서 사용하는 첨자를 2.

응력과 변형률 Metal Forming CAE Lab. Department of Mechanical Engineering – ppt download

인장시험, 재료의 거시적 거동 특성

  • Image source: slidesplayer.org
  • Views: 19799
  • Publish date: 36 minute ago
  • Downloads: 11839
  • Likes: 2307
  • Dislikes: 1
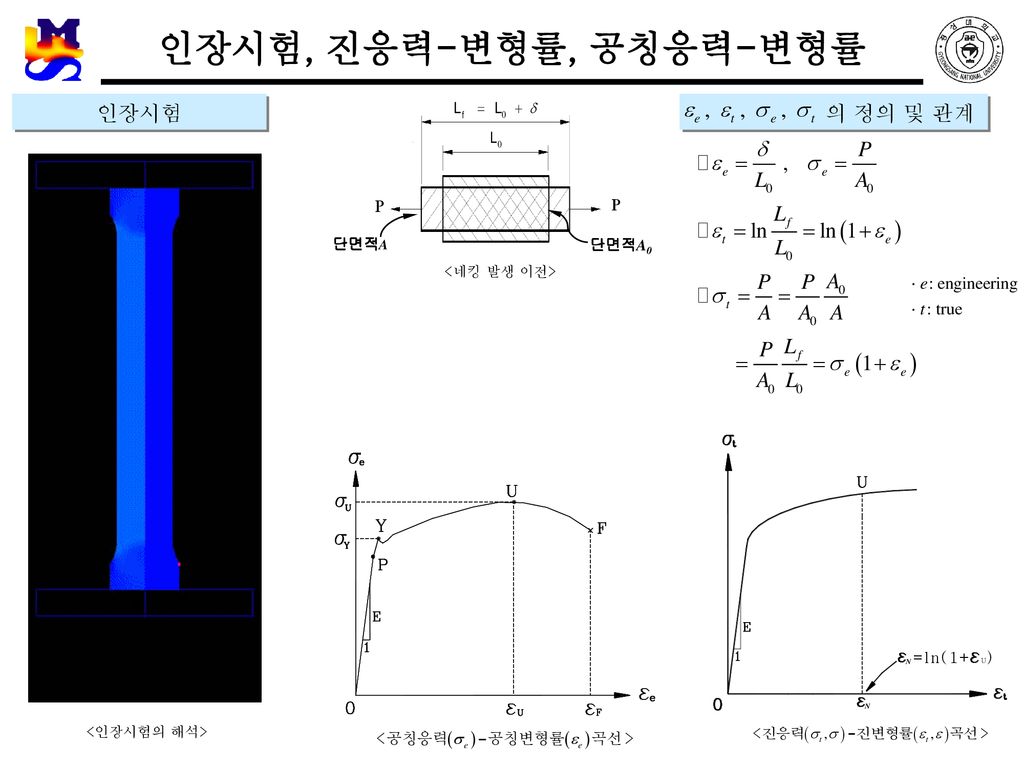
응력과 변형률 Metal Forming Cae Lab. Department Of Mechanical Engineering - Ppt Download
응력과 변형률 Metal Forming Cae Lab. Department Of Mechanical Engineering – Ppt Download

한 면을 x축과 일치시키고, 그림처럼 그 면과 반대편 면에 sigma xx의 응력을 분포시키면, x방향으로는 sigma xx/E(이 분의 시그마 엑스엑스) 만큼의 변형률이 발생하고, y축과 z축으로는 재료의 고유 특성치인 Poisson(포아송)비만큼, 즉 -mu epsilon xx(마이너스 뮤 잎실론 엑스엑스)만큼의 변형률이 발생합니다.

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

1. 2 차원 배열  배열은 동일한 데이터 유형으로 여러 개의 변수를 사용할 경우 같은 이 름으로 지정하여 간편하게 사용할 수 있도록 하는 것으로서 앞에서 1 차원 배열을 공부하였습니다.  2 차원 배열은 바둑판을 생각하면 되며, 1 차원 배열에서 사용하는 첨자를 2.

훅 뜻: 영국의 물리학자ㆍ천문학자(1635~1703). 직접 만든 현미경으로 세포를 발견하고, 천체

훅: 영국의 물리학자ㆍ천문학자(1635~1703). 직접 만든 현미경으로 세포를 발견하고, 천체의 운행이나 광학적 현상을 연구하여 빛의 파동설을 제창하였다. 탄성(彈性)에 관한 ‘훅의 법칙’을 발견하였으며, 코르크 조각의 세포를 관찰하여 세포를 ‘셀(cell)’이라고 이름 (어휘 명사 외래어 인명 )

  • Image source: wordrow.kr
  • Views: 44331
  • Publish date: 10 minute ago
  • Downloads: 53121
  • Likes: 308
  • Dislikes: 1
훅 뜻: 영국의 물리학자ㆍ천문학자(1635~1703). 직접 만든 현미경으로 세포를 발견하고, 천체
훅 뜻: 영국의 물리학자ㆍ천문학자(1635~1703). 직접 만든 현미경으로 세포를 발견하고, 천체

하, 학, 한, 할, 핡, 함, 합, 핫, 항, 해, 핵, 핸, 햄, 햇, 행, 향, 허, 헉, 헌, 헐, 험, 헛, 헝, 헤, 헥, 헬, 헴, 헵, 헷, 헹, 혀, 혁, 현, 혈, 혐, 협, 형, 혜, 혬, 호, 혹, 혼, 홀, 홈, 홉, 홍, 홑, 화, 확, 환, 활, 황, 홰, 홱, 횅, 회, 획, 횟, 횡, 효, 후, 훅, 훈, 훌, 훍, 훔, 훗, 훙, 훠, 훤, 훨, 훰, 훼, 휀, 휑, 휘, 휙, 휠, 휨, 휭, 휴, 흄, 흉, 흐, 흑, 흔, 흘, 흙, 흠, 흥, 흨, 희, 힁, 히, 힐, 힘, 힝, 힠

녹아웃 훅, 쇼트 훅, 버튼 훅, 피시 훅, 스카이 훅, 리드 훅, 셰퍼드 훅, 진훅, 스카이훅, 힐 훅, 갈고리 훅, 넉아웃 훅, 오프훅, 펠리컨 훅, 어저스터블 훅, 핸드 라인 훅, 도체 인상 훅, 섬유 훅, 러시안 훅, 라이트 훅, 스테이 훅, 그래브훅, 퀵 훅, 레이우엔훅, 니들 훅, 스위치 훅, 레프트 훅, 훅, 온훅, 더크 훅, 피피 훅, 캠 훅, 유지 보수 훅, 미트 훅, 훅훅, 게훅, 교환 훅 …

녹아웃 훅, 쇼트 훅, 버튼 훅, 피시 훅, 스카이 훅, 리드 훅, 셰퍼드 훅, 진훅, 스카이훅, 힐 훅, 갈고리 훅, 넉아웃 훅, 오프훅, 펠리컨 훅, 어저스터블 훅, 핸드 라인 훅, 도체 인상 훅, 섬유 훅, 러시안 훅, 라이트 훅, 스테이 훅, 그래브훅, 퀵 훅, 레이우엔훅, 니들 훅, 스위치 훅, 레프트 훅, 훅, 온훅, 더크 훅, 피피 훅, 캠 훅, 유지 보수 훅, 미트 훅, 훅훅, 게훅, 교환 훅 …

고객의 습관을 독점하는 플랫폼 전략, ‘훅모델’

#8 Hook Modelㅣ외부계기

  • Image source: maily.so
  • Views: 6829
  • Publish date: 18 hours ago
  • Downloads: 14915
  • Likes: 8650
  • Dislikes: 5
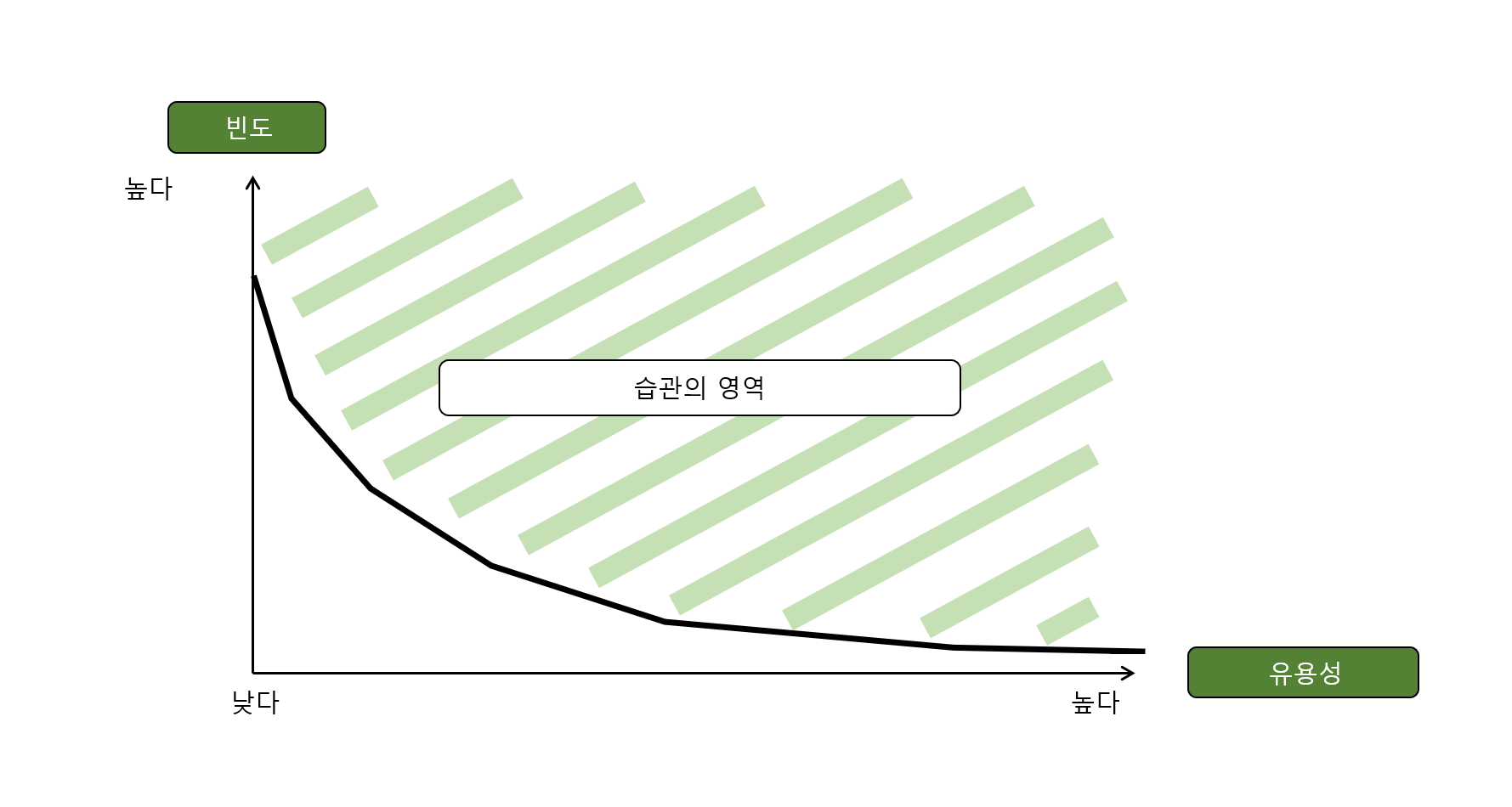
고객의 습관을 독점하는 플랫폼 전략, '훅모델'
고객의 습관을 독점하는 플랫폼 전략, ‘훅모델’

플랫폼에 과연 모델링이 존재할 수 있을까, 의미가 있는 것인가, 세계적인 위치에 올라간 모든 플랫폼은 과연 이런 모델링에 기초하여 빌딩된 것일까, CEO나 기획자의 감각적인 기획에 의해 이뤄지는 것은 아닌가, 한 번에 완성된 플랫폼이란 존재하지 않고, 부족한 채로 탄생하였지만 고객을 관찰하고, 개선되면서 지금의 서비스가 만들어진 것은 아닐까 등등의 이러한

지금까지 외부계기, 즉 외부환경을 통해 고객이 우리 서비스를 인지하고 행동 (다운로드, 재방문, 탐색, 기타 등등) 하게 하는 방법에 대해 말씀 드렸습니다. 플랫포머로써 우리가 어떻게 외부계기를 만들어야 효과적으로 고객 행동을 유도할 수 있는지 고민하는 과정에서 이러한 모델링을 참조하시면 좋을 것 같아요.

이런 글로벌 서비스를 사용하는 것처럼, 의식없이 습관적으로 행동하는 경우가 많다는 거죠. 인스타그램을 하는 우리의 행위를 엿보면, 사실 의식적으로 인스타그램을 켜기 보다, 누군가를 기다리다가, 또는 심심해서 무의식적으로 인스타그램을 보는 경우가 많습니다. 유튜브도 마찬가지고요.

비디오 훅 의 법칙 (재료역학) 제9강 훅의법칙(후크의법칙)과 탄성계수

  • Source: Youtube
  • Views: 60383
  • Date: 18 minute ago
  • Download: 87181
  • Likes: 223
  • Dislikes: 2

주제에 대한 관련 정보 훅 의 법칙

Bing에서 훅 의 법칙 주제에 대한 최신 정보를 볼 수 있습니다.

훅의 법칙 나무위키

훅의 법칙 텐서

훅의 법칙 탄성계수

훅의 법칙 유도

후크 법칙

용수철 상수

훅의 법칙 문제

탄성력 공식

주제에 대한 기사 보기를 마쳤습니다 훅 의 법칙. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.

훅의 법칙 나무위키

훅의 법칙 텐서

훅의 법칙 탄성계수

훅의 법칙 유도

후크 법칙

용수철 상수

훅의 법칙 문제

탄성력 공식

Leave a Comment