톱 218 사인 코사인 표 업데이트 22 일 전

사인 코사인 변환

Sin cos, tan 공식

사인 코사인 탄젠트 관계

사인, 코사인, 탄젠트

Sin 표

사인, 코사인, 탄젠트 공식

사인 코사인 탄젠트 변환

삼각함수 공식

주제에 대한 기사를 찾고 있습니까 “사인 코사인 표“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: c2.castu.org/blog. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.

이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.

컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.

Table of Contents

사인 코사인 표 주제와 관련된 상위 126 이미지

주제 사인 코사인 표 와 관련된 8 개의 이미지가 있습니다.

SIN COS TAN 표, 쉽게 외우는 방법

안녕하세요. 오늘은 SIN COS TAN 특수각의 삼각비를 쉽게 암기하는 방법에 대한 내용으로 포스팅을 합니다. 목차 – SIN COS TAN 특수각의 삼각비 표 – 한번에 암기하는 방법 수학 중에 삼각함수를 어려워하는 분들이 많은 걸로 알고 있는데요. 특히, 삼각함수의 특수각의 삼각비는 수학 문제에서 정말 많이 활용되는 값으로 꼭 알아두셔야 합니다. SIN COS TAN 특수각의 삼각비 표 우선 ‘특수각’이란 0, 30, 45, 60, 90도를 의미하는데요. 수학 문제에서도 자주 사용되며, 실제 공학 계산에서도 대표되는 각도이기 때문에 ‘특수각’이라는 이름이 붙게 되었습니다. 실제 활용이 높다 보니 해당 특수각의 삼각비 값을 표로 암기하는데요. 아래는 삼각함수의 특수각의 삼각비 값입니다. 한 번에 암기..

Image source: qktkdu.tistory.com
Views: 35698
Publish date: 14 hours ago
Downloads: 60703
Likes: 1887
Dislikes: 7

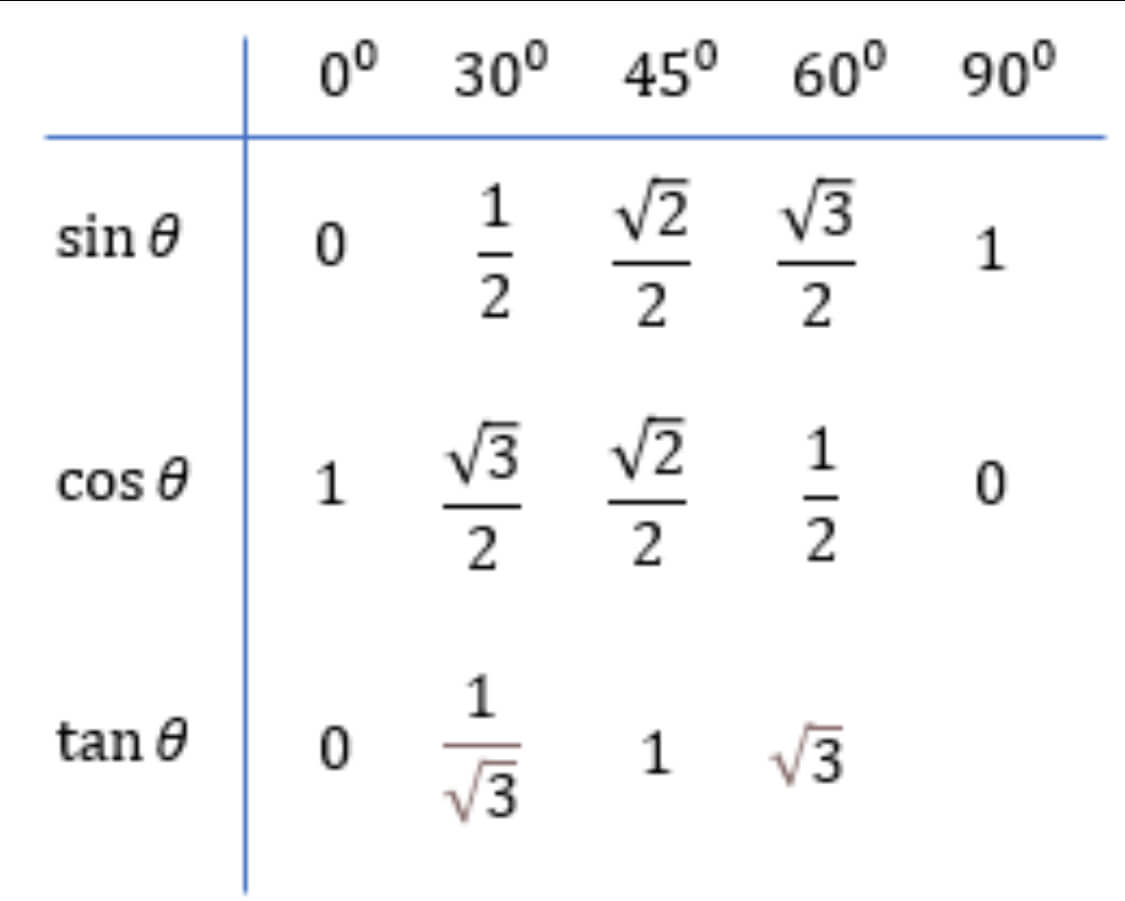
특수각의 삼각비는 규칙성이 있는데요. 규칙성만 알고 있으면, 쉽게 외우 수 있습니다. SIN 함수의 경우는 분모는 2로 고정이고 분자가 루트 0~4까지 증가하는 규칙성이 있고 COS는 반대로 분자가 루트 4에서 0으로 감소하는 규칙성이 있습니다. TAN의 경우는 0부터 시작해서 루트 3씩 곱해지는 규칙성이 있으니, 이런 규칙성을 기억하시면 좋을 것 같습니다.

우선 ‘특수각’이란 0, 30, 45, 60, 90도를 의미하는데요. 수학 문제에서도 자주 사용되며, 실제 공학 계산에서도 대표되는 각도이기 때문에 ‘특수각’이라는 이름이 붙게 되었습니다. 실제 활용이 높다 보니 해당 특수각의 삼각비 값을 표로 암기하는데요. 아래는 삼각함수의 특수각의 삼각비 값입니다.

그리고 시험이라 모의고사 때 추천드리는 방법은 시험지에 우선 암기한 특수각의 삼각비 표를 적어 놓는 것을 추천드립니다. 시험에서 특수각의 삼각비는 반드시 사용되니까요.

SIN COS TAN 표 삼각비 인쇄용 PDF 파일 다운로드 – 폭스씨지 FoxCG

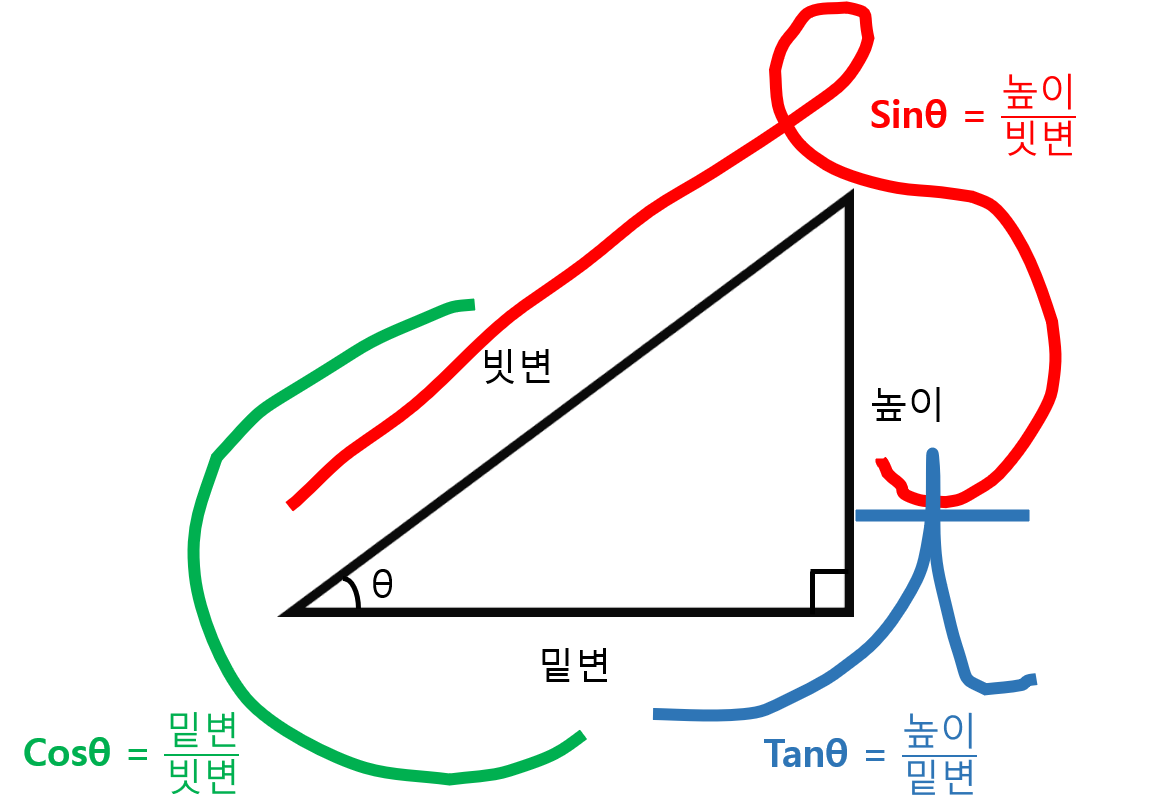
"SIN COS TAN 표 삼각비 인쇄용 PDF 파일 다운로드" 삼각비는 직각삼각형의 세 변의 길이 중 두 변의 길이 간의 비례 관계를 나타내는 값을 말합니다. 삼각비는 직각삼각형의 각 변의 비율을 수식으로 표현한 것으로 중등수학에서 다루고 있습니다. 고등학교 수학과정 까지 계속 이어지는 중요한 공식으로 반드시 알아두어야 할 중요한 수식입니다. $$ sin \theta = \frac{높이}{빗변} $$ $$ cos \theta = \frac{밑변}{빗변} $$ $$ tan \theta = \frac{높이}{밑변} $$ 위와 같이 Sin, Cos, Tan 맨 앞글자 스펠링을 이용해서 암기하는 방법도 있습니다. "SIN COS TAN 표 삼각비 인쇄용 PDF 파일 다운로드" 각 변의 비례 관계는 위의 식으로..

Image source: foxcg.com
Views: 6334
Publish date: 52 minute ago
Downloads: 99022
Likes: 1312
Dislikes: 7

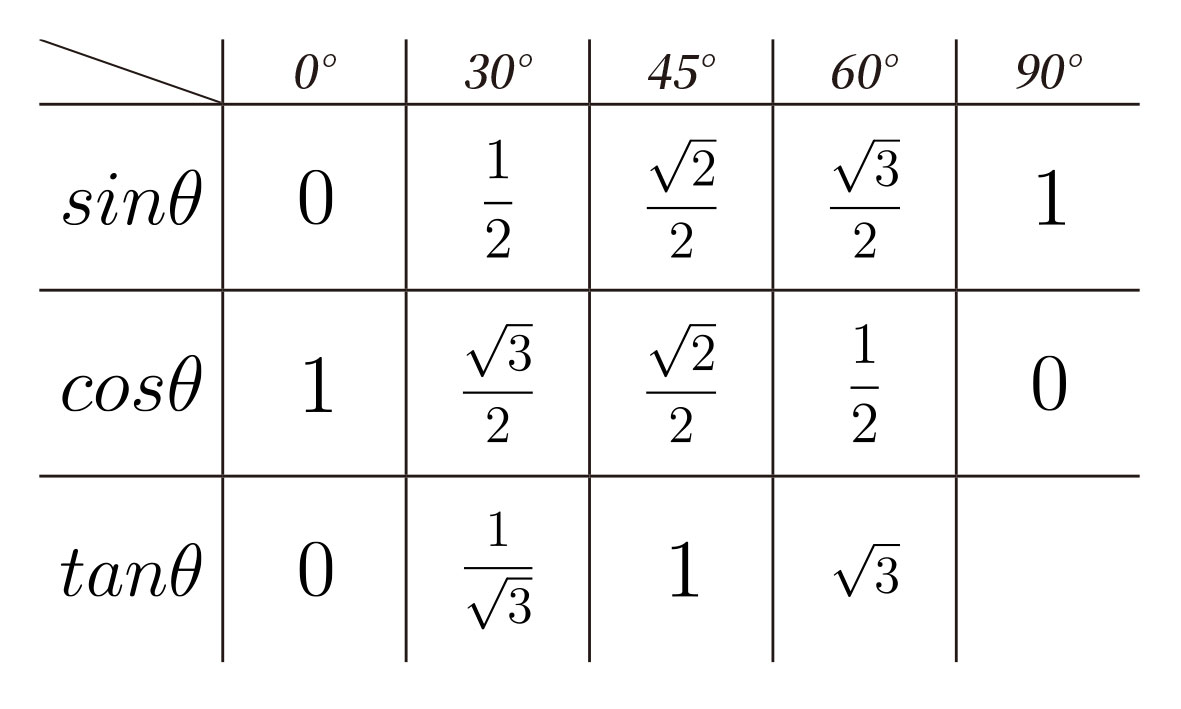
Sin Cos Tan 표 삼각비 인쇄용 Pdf 파일 다운로드 - 폭스씨지 Foxcg — Sin Cos Tan 표 삼각비 인쇄용 Pdf 파일 다운로드 – 폭스씨지 Foxcg

삼각비는 직각삼각형의 각 변의 비율을 수식으로 표현한 것으로 중등수학에서 다루고 있습니다. 고등학교 수학과정 까지 계속 이어지는 중요한 공식으로 반드시 알아두어야 할 중요한 수식입니다.

각 변의 비례 관계는 위의 식으로 표현할 수 있습니다. 임의의 각 θ 를 기준으로 위의 관계를 표로 정리한 것이 SIN COS TAN 표 즉, 삼각비 표 입니다.

삼각비는 직각삼각형의 세 변의 길이 중 두 변의 길이 간의 비례 관계를 나타내는 값을 말합니다.

삼각비 표(0도~180도)를 만들어봤어요.

예전에는 수학문제집 뒤에 다 붙어있었던 것 같은데, 필요해서 찾으니 자료를 찾기 쉽지 않네요. 그림파일로 몇개 찾았는데, 생각난 김에 엑셀을 써서 만들어봤습니다. 참고로 엑셀에서는 sin, cos, tan 함수를 활용했는데, 입력값으로 라디안 각도를 사용합니다. 더 쉬운 방법도 분명 있을 것 같은데 할 수 있는 방법으로 만들어봤습니다. 0도에서 90도까지가 쓰임이 많을 것 같아 A4 사이즈에 맞춘 pdf파일 첨부합니다. 필요하신 분은 인쇄해서 사용하세요. 삼각비 표 활용 방법 만약 60도에 대한 코사인 값을 찾는다면, 각도수치에서 60도를 찾고(파란색 가로줄), 코사인 컬럼(분홍색 세로줄)이 교차하는 지점의 값을 보면 됩니다. 60도의 코사인 값은 1/2로 많이 외우는 값이고, 삼각비 표에서는 0.5로 ..

Image source: lucia.tistory.com
Views: 1398
Publish date: 12 hours ago
Downloads: 26700
Likes: 4624
Dislikes: 10

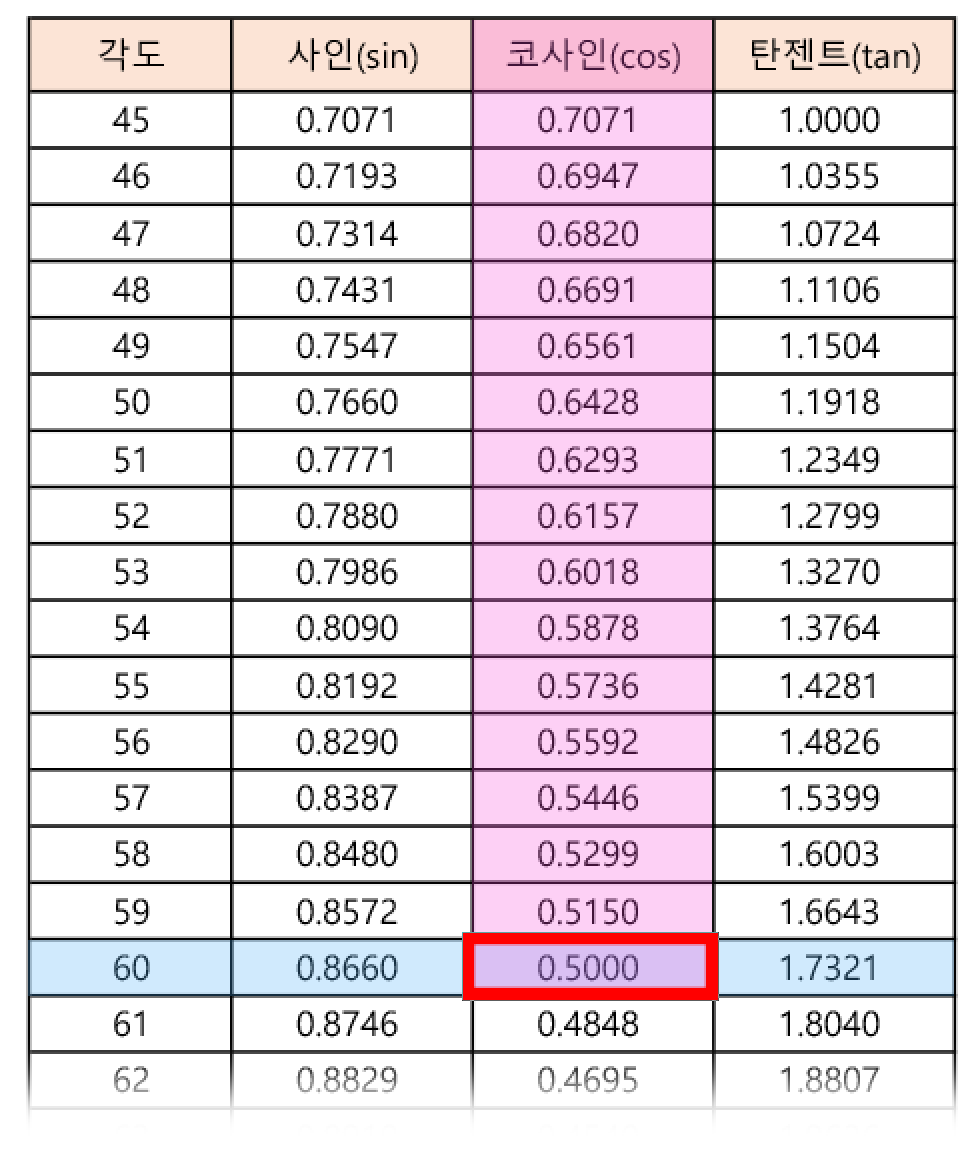
만약 60도에 대한 코사인 값을 찾는다면, 각도수치에서 60도를 찾고(파란색 가로줄), 코사인 컬럼(분홍색 세로줄)이 교차하는 지점의 값을 보면 됩니다. 60도의 코사인 값은 1/2로 많이 외우는 값이고, 삼각비 표에서는 0.5로 표시된 것을 확인할 수 있습니다.

참고로 엑셀에서는 sin, cos, tan 함수를 활용했는데, 입력값으로 라디안 각도를 사용합니다. 더 쉬운 방법도 분명 있을 것 같은데 할 수 있는 방법으로 만들어봤습니다.

[정시] 2023학년도 성균관대 최초합격자 등록기간 2월 7일~9일 : 전년도(2022학년도) 정시 경쟁률, 충원율 자료 살펴보기

수학] 코사인 개념 설명 그래프, Cos Cosine 의미 개념도 Graph 차트

Image source: mwultong.blogspot.com
Views: 2883
Publish date: 8 minute ago
Downloads: 100261
Likes: 2789
Dislikes: 4

간단한 프로그래밍(기초적인 코딩 위주) 예제 소스 코드와 언어들의 기초 강좌, 소프트웨어, 웹 디자인과 관련된 내용. 그래픽에 쓸 수 있는 색상표와, 각종 프로그램들의 사용법 설명, 웹 브라우저에서 각종 단위를 환산하는 계산기/변환기 등.

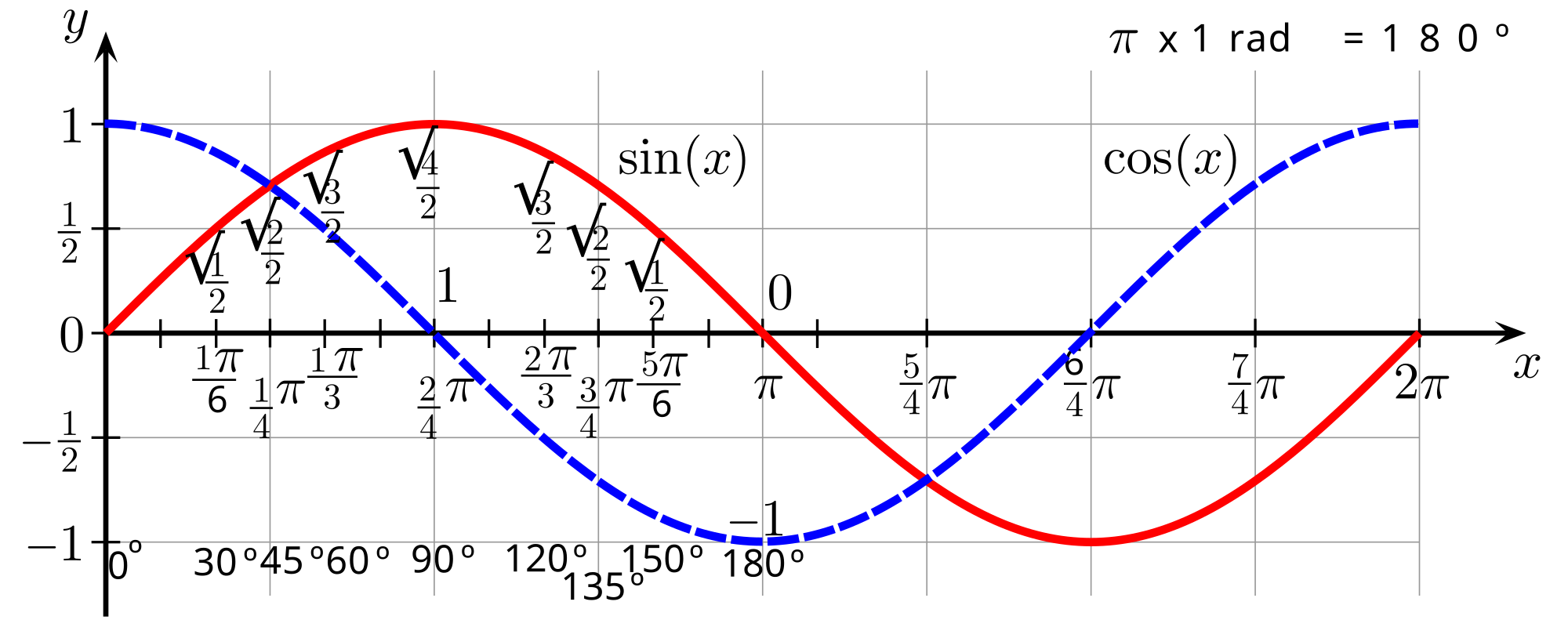
삼각함수에서 코사인이란, 아래 그래프에서 빨간 수평선입니다. 빨간 수평선의 길이를 코사인 값이라고 합니다. 각도를 나타내는 파란 직선이 회색 원주와 만나는 지점과, y축을 수평으로 이어준 것이 빨간 수평선입니다.

위의 그래프에서 뻔데기 기호인 세타(θ)는 각도를 의미합니다. 다만 360도의 각도가 아니라, 라디안 단위입니다. 그렇지만 위의 그래프는 이해를 쉽게 하기 위해서 일반적인 360도 각도로 표현했습니다.

삼각비 표(0도~180도)를 만들어봤어요.

Image source: lucia.tistory.com
Views: 86300
Publish date: 49 minute ago
Downloads: 24586
Likes: 7601
Dislikes: 1

[정시] 2023학년도 성균관대 최초합격자 등록기간 2월 7일~9일 : 전년도(2022학년도) 정시 경쟁률, 충원율 자료 살펴보기

삼각함수 – 위키백과, 우리 모두의 백과사전

Image source: ko.wikipedia.org
Views: 87958
Publish date: 4 hours ago
Downloads: 53525
Likes: 3033
Dislikes: 10

코사인법칙은 두 변의 길이와 끼인각의 크기를 알 때 삼각형의 나머지 한 변의 길이를 구할 때 유용하게 쓸 수 있다. 또한 모든 변의 길이를 알고 있을 때 각의 코사인값을 구할 때에도 사용할 수 있다.

{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan {{1 \over 2}(A+B)}}{\tan {{1 \over 2}(A-B)}}}}

{\displaystyle \cot \theta ={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}}

수학] 사인 함수 개념 설명 그림, 삼각함수에서 Sin Sine 싸인 함수 그래프 Graph

Image source: mwultong.blogspot.com
Views: 49431
Publish date: 4 minute ago
Downloads: 40037
Likes: 1782
Dislikes: 5

수학의 다른 분야도 그렇지만 삼각함수는, 말로 설명하면 이해가 잘 안됩니다. 그림을 봐야 합니다. 삼각함수에서 사인이란, 아래 그래프에서 빨간 수직선입니다. 빨간 수직선의 길이를 사인 값이라고 합니다. 각도를 나타내는 파란 직선이 회색 원주와 만나는 지점과, x축을 수직으로 이어준 것이 빨간 수직선입니다.

사인함수에 입력하는 각도는 보통의 360도 각도가 아니라, 라디안(Rad) 단위여야 합니다. 그러나 위의 원 그래프들은 이해를 돕기 위해 360도 각도 단위를 붙여 놓았습니다.

sin cos tan 표 쉽게 암기하는 방법(특수각의 삼각비 표 절대 잊지 않는 법)

삼각함수에 대해 공부하는 학생이라면 sin cos tan 표에 대해 암기를 하고 있어야 합니다. 특수각에 대한 값이 복잡하지는 않기 때문에 외우는데 크게 어려움은 없지만 쉽게 암기하는 방법으로 머릿속에 정확히 집어넣는 것이 중요합니다. sin cos tan 표 삼각비 표 특수각은 아래 표(sin cos tan 표)와 같습니다. 암기 쉽게 하는 방법 1. Sin의 경우에 분모가 모두 2이며, 분자에는 순서대로 루트 1, 루트 2, 루트 3이라고 외우시면 됩니다. 2. Cos의 경우네는 Sin의 순서에서 반대라고 기억하시면 됩니다. 3. Tan은 Tan30이 1/√3라는 것만 외우시고 오른쪽으로 갈수록 √3을 곱한 값과 같다고 생각하시면 됩니다. 위의 방법대로 암기하면 절대 잊어버리지 않을거라 생각합니다. ..

Image source: gordonoliver.tistory.com
Views: 47030
Publish date: 2 hours ago
Downloads: 98394
Likes: 8836
Dislikes: 5

Sin Cos Tan 표 쉽게 암기하는 방법(특수각의 삼각비 표 절대 잊지 않는 법)

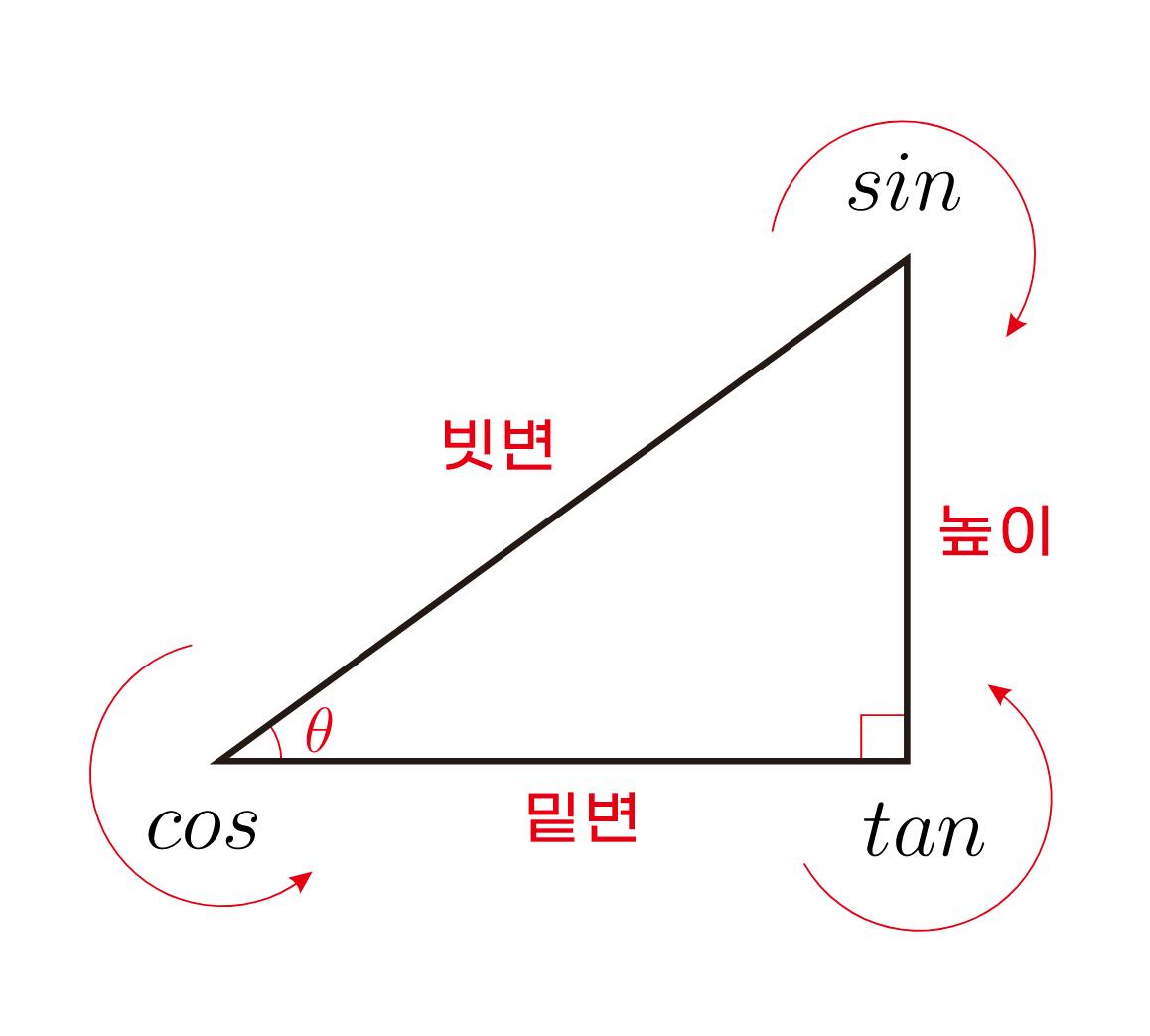
θ의 경우에는 빨간선을 생각하면서 그리면 오른쪽에 Sin의 S가 보이죠? 빨간 선은 빗변에서 시작해 높이에서 끝났는데요. 시작한 쪽이 분모로 가고 끝나는 쪽이 분자로 간다고 생각하시면 됩니다.

Tanθ의 경우에는 파란선을 생각하면서 그리면 모양이 Tan의 T처럼 보입니다. 파란선이 밑변에서 시작해 높이에서 끝났으니 사직한 쪽을 분모, 끝나는 쪽을 분자로 두면 높이/밑변이 됩니다.

θ의 경우에는 녹색선을 생각하면서 그리면 모양이 Cos의 C처럼 보입니다. 녹색선이 빗변에서 시작해 밑변에서 끝났으니 시작한 쪽을 분모, 끝나는 쪽을 분자로 두면 밑변/빗변이 됩니다.

KR20110015026A – ì¬ì¸ ë° ì½ì¬ì¸ ë°ìê¸°
– Google Patents

Image source: patents.google.com
Views: 30318
Publish date: 20 hours ago
Downloads: 57952
Likes: 4105
Dislikes: 2

Kr20110015026A - 사인 및 코사인 발생기 - Google Patents — Kr20110015026A – 사인 및 코사인 발생기 – Google Patents

ì ì¬íê², ê±°ì¹ê° Aì ì¬ì¸ì ì 2 ê³ì° ë¨ê³(110) ëì ê²°ì ë ì ìë¤. ì¬ì¸ ê²°ì ì ì¼ë°ì ì¼ë¡ ê±°ì¹ê° Aì ì¬ì¸ì ê³ì°íê±°ë ëë ê±°ì¹ê° Aì ì¬ì¸ì ëí ë¯¸ë¦¬ ê³ì°ë ê°ë¤ì ì ííê¸° ìí´ íìí ìëì ìííë ê²ì í¬í¨í ì ìë¤. ê·¸ë° íì, ê±°ì¹ê° Aì ì¬ì¸ì ìµìì ë¨ì´ë¡ ë° ìµíì ë¨ì´ ë¡ ë¶í´ëë¤. ë¶í´ íë¡ì¸ì¤ë sin(A)ì ìµìì ë¨ì´() ë° sin(A)ì ìµíì ë¨ì´()ì ëí ê°ì ê³ì°íë ê²ì ì¼ë°ì ì¼ë¡ í¬í¨í ì ìë¤. ëìì ì¼ë¡, ë¶í´ íë¡ì¸ì¤ë ë°/ëë ì ëí ë¯¸ë¦¬ ê³ì°ë ê°ë¤ì ì ííê¸° ìí´ íìí ìëì ìííë ê²ì í¬í¨í ì ìë¤. ì¬ì¸ ê²°ì ë° ë¶í´ íë¡ì¸ì¤ë ë°/ëë ì ëí ë¯¸ë¦¬ ê³ì°ë ê°ë¤ì ì ííê¸° ìí´ íìí ìëì ìííë ê²ì ì§í©ì ì¼ë¡ í¬í¨í ì ìë¤ë ì ì´ ì¸ê¸ëì´ì¼ë§ íë¤.

ë ¥ê°()ì ì¬ì¸ ë° ì½ì¬ì¸ì ë°ìíê¸° ìí ë°©ë²(300). ê·¸ ë°©ë²ì ì ì¥íí¸ ëë ì¿¼ëë°í¸, ê±°ì¹ê°(A), ë° ë¯¸ì¸ê°(B)ì¼ë¡ ë¶í´íë ë¨ê³, cos(A)ì ê²°ì íë ë¨ê³, ë° sin(A)ì ê²°ì íë ë¨ê³ë¥¼ í¬í¨íë¤. ë°©ë²ì ëí ìµìì ë¨ì´(MSW) ë° ìµíì ë¨ì´(LSW)ë¡ cos(A) ë° sin(A)ì ë¶í´íë ë¨ê³ë¥¼ í¬í¨íë¤. ê·¸ ë°©ë²ì 1-cos(B)ì ê·¼ì¬ì¹, sin(B)ì ê·¼ì¬ì¹, ë° MSWë¤ì ì¬ì©íë ë³µìì íë¡ëí¸ë¤ ë° ê·¼ì¬ì¹ë¤ì ê³ì°íë ë¨ê³ë¥¼ ë í¬í¨íë¤. ê·¸ ë°©ë²ì cos(A), sin(A), ë° ì ëí ê°ë¤ì ì¬ì©íì¬ cos() ë° sin()ì ê·¼ì¬ì¹ë¥¼ ê³ì°íë ë¨ê³ë¥¼ í¬í¨íë¤. ê·¸ ë°©ë²ì ìíë í´ë²ì¼ë¡ cos() ë° sin()ì ê·¼ì¬ì¹ë¤ì ì¤ì¼ì¼ë§íë ë¨ê³ë¥¼ í¬í¨íë¤.

조금은 느리게 살자: 삼각 함수(三角函數, Trigonometric Function)

Image source: ghebook.blogspot.com
Views: 22494
Publish date: 27 minute ago
Downloads: 1070
Likes: 7390
Dislikes: 4

이기 때문에 밑변과 높이가 서로 같다. 따라서 큰 직각 삼각형과 작은 직각 삼각형의 삼각비는 서로 같다. 비슷한 논리로 [그림 3(b)]의 오른쪽 직각 삼각형처럼 빗변을 등간격으로 $m$등분해서 각 점을 기준으로 밑변과 높이에 평행한 선을 긋는다. 그러면 밑변과 높이도 빗변과 같이 등간격으로 균등하게 나누어짐을 볼 수 있다. 즉 빗변 분할로 생긴 임의의 직각 삼각형은 서로 닮아있고 변의 비율도 같다. 이로 인해 원래 직각 삼각형과 $m$등분으로 생긴 임의의 직각 삼각형의 삼각비는 항상 동일하다. 예를 들어, 빗변 길이가 $10$인 직각 삼각형과 닮은 빗변 길이가 $1.2$인 직각 삼각형을 비교해본다. 두 삼각형의 빗변 비율이 $10:1.2$ = $25:3$이므로, [그림 3(b)]의 오른쪽 삼각형처럼 길이가 $10$인 빗변을 25등분해서 균등한 길이 조각을 25개 만든다. 꼭지점부터 헤아려서 처음 3개 길이 조각이 구성하는 직각 삼각형은 빗변이 $1.2$이다. 그러면 ASA 합동에 의해 등간격으로 나눈 두 삼각형의 삼각비는 완전히 같다. 결국 직각 삼각형의 빗변을 등간격으로 나누는 과정은 매우 작은 길이까지 계속 진행될 수 있으므로, 모든 닮은 직각 삼각형의 삼각비는 항상 같다.

거북이님… 보다가 이해 안가는 부분이 있어서 질문드립니다. (4) (5) 번 식을 대수기하학으로 증명하는 과정에서 갑자기 x_1,2 = b1,2/h1,2 와 y_1,2 = a1,2/h1,2 를 이용해 x_1^2+y_1^2=1 을 유도하고 있는데, x_1,2 의 정의가 무엇인지와 어떻게 원의 방정식이 유도되었는지 많은 내용이 생략되어 이해하기 힘드네요… 대수기하학이 뭔지 몰라 위키피디아를 살펴보아도 x1,2 와 같은 정의는 없네요… 바쁘시겠지만 간략하게 보충설명해주시면 감사하겠습니다.

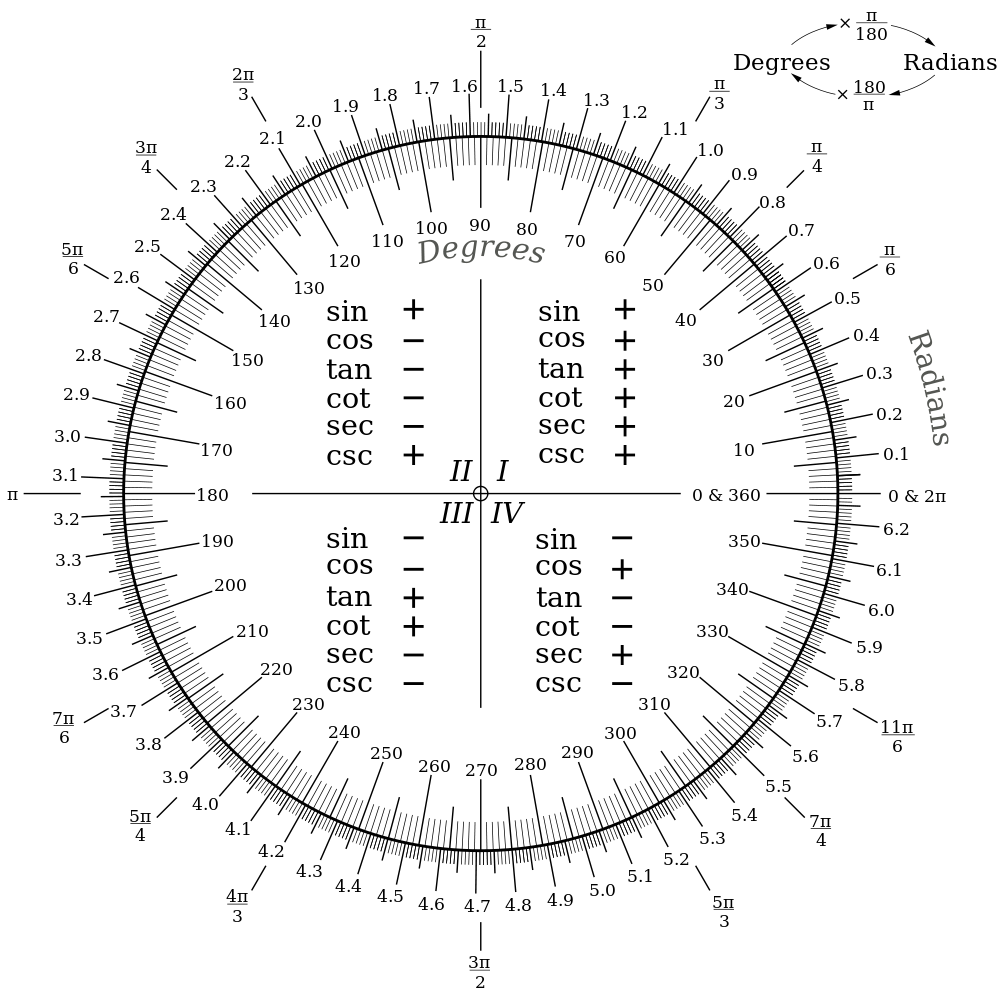
, $\theta$는 라디안으로 정의한 각도, $\vartheta$는 360˚ 기준 각도이다. 식 (21)의 우변 식은 라디안 $\theta$를 360˚ 기준 $\vartheta$로 바꾸기를 의미한다. 예를 들어, $\theta = \pi$ rad를 대입하면 $\vartheta = 180/\pi \cdot \pi = 180^\circ$를 얻을 수 있다. 자세한 라디안과 각도 관계는 [표 1]을 참고한다.

[삼각비] 특수각 사인, 코사인, 탄젠트 15º, 75º, 22.5º, 67.5º

삼각비의 특수각은 0º, 30º, 45º, 60º, 90º까지는 외워서 쓰죠. 그리고 미적분에서 삼각함수의 덧셈정리를 배우고 나면, 15º=45º-30º 75º=45º+30º 22.5º=45º/2 67.5º=45º+22.5º or 90º-22.5º 이런 식으로 특수각들로 만들 수 있는 다른 각도 삼각비의 값을 구할 수 있답니다. 그렇지만 오늘의 카테고리는 중등 3학년 삼각비! 그래서 도형으로 해당 값들을 유도해서 풀어볼거에요. 중3 삼각비 15도, 75도 유도 기본은 우리가 아는 30º, 60º, 90º로 이루어진 직각 삼각형과 직각 이등변 삼각형 두 개를 붙여놓은 걸로 시작합니다. 처음부터 미지수를 쓰면 눈에 잘 안 들어올 수 있으니 간단하게 숫자로 설명하고 일반화하도록 할게요! 아래 그림과 같이 BE..

Image source: ladyang86.tistory.com
Views: 96830
Publish date: 36 minute ago
Downloads: 81210
Likes: 2950
Dislikes: 2

삼각비] 특수각 사인, 코사인, 탄젠트 15º, 75º, 22.5º, 67.5º

기본은 우리가 아는 30º, 60º, 90º로 이루어진 직각 삼각형과 직각 이등변 삼각형 두 개를 붙여놓은 걸로 시작합니다. 처음부터 미지수를 쓰면 눈에 잘 안 들어올 수 있으니 간단하게 숫자로 설명하고 일반화하도록 할게요!

BFE와 FGE 역시 직각 이등변 삼각형이기 때문에 길이를 모두 구할 수 있습니다. 여기서 FEDC는 직사각형이므로 CD의 길이도 구할 수 있고, 이걸 AD에서 빼면 AC의 길이도 구할 수 있습니다.

중3 2학기 내용은 고등학교 입시에 영향 덜하다고 대충 넘기고 고1 선행을 하지 마시고, (이러면 나중에 고2때 다시 중3 수학 해야 한답니다..?) 현재에 충실히 공부하시길 응원합니다.

SIN COS TAN 표 삼각비 인쇄용 PDF 파일 다운로드 – 폭스씨지 FoxCG

Image source: foxcg.com
Views: 95718
Publish date: 19 hours ago
Downloads: 36766
Likes: 5308
Dislikes: 6

각 변의 비례 관계는 위의 식으로 표현할 수 있습니다. 임의의 각 θ 를 기준으로 위의 관계를 표로 정리한 것이 SIN COS TAN 표 즉, 삼각비 표 입니다.

삼각비는 직각삼각형의 세 변의 길이 중 두 변의 길이 간의 비례 관계를 나타내는 값을 말합니다.

삼각함수 미분 도함수 그래프, 사인 코사인 탄젠트 미분하기; Derivative Sin Cos Tan

Image source: mwultong.blogspot.com
Views: 105244
Publish date: 8 hours ago
Downloads: 15734
Likes: 9203
Dislikes: 8

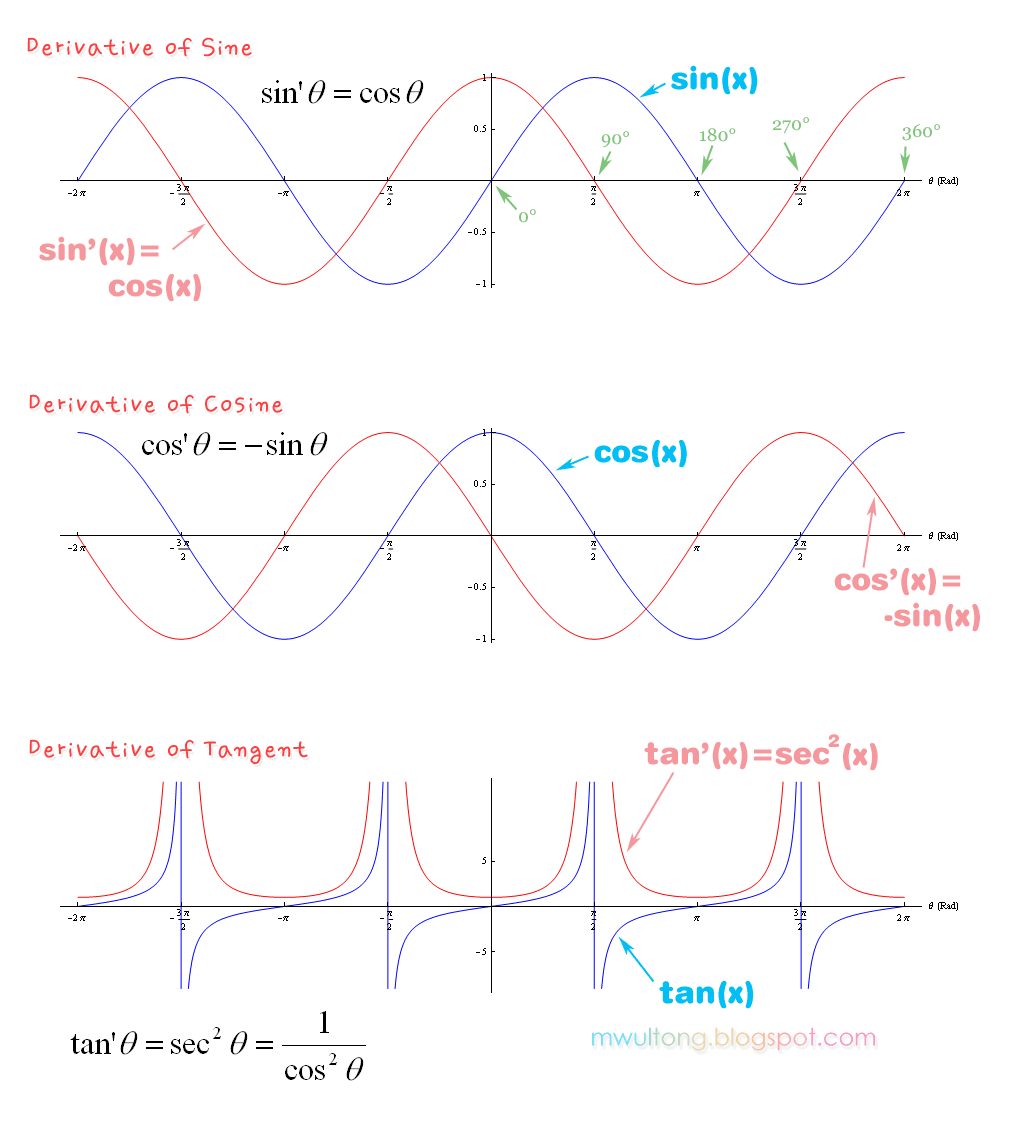
삼각함수에서, 사인을 미분하면 코사인이 되고, 코사인을 미분하면 “마이너스 사인”이 되고, 탄젠트를 미분하면 “시컨트 제곱”이 됩니다. 그런데 이런 것을 외우기만 하려면 금방 잊어 버리게 됩니다. 따라서 그래프를 보며 이해를 하는 것이 좋습니다.

아래 그래프는 마이너스 360도 즉 마이너스 2파이 라디안에서, 플러스 360도 즉 2파이 라디안까지 각도의 그래프입니다. 파란 선은 원래의 함수의 곡선이고, 빨간 선은 미분한 결과 즉 도함수의 그래프입니다.

Image source: www.shutterstock.com
Views: 19272
Publish date: 23 hours ago
Downloads: 25443
Likes: 7997
Dislikes: 5

Sin Cos Tan Pythagoras Formula White 스톡 일러스트 1629403255 | Shutterstock

Image source: rikeinvest.com
Views: 31768
Publish date: 12 minute ago
Downloads: 91213
Likes: 9288
Dislikes: 8

삼각 함수 표의 코사인 표에서 Cos74 °를 구하는 방법 | Tomlab

비디오 사인 코사인 표 삼각함수의 값 쉽게 구하기

여기에서 비디오 보기

Source: Youtube
Views: 13827
Date: 15 hours ago
Download: 29486
Likes: 1255
Dislikes: 2

주제에 대한 관련 정보 사인 코사인 표

Bing에서 사인 코사인 표 주제에 대한 최신 정보를 볼 수 있습니다.

사인 코사인 변환

Sin cos, tan 공식

사인 코사인 탄젠트 관계

사인, 코사인, 탄젠트

Sin 표

사인, 코사인, 탄젠트 공식

사인 코사인 탄젠트 변환

삼각함수 공식

주제에 대한 기사 보기를 마쳤습니다 사인 코사인 표. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.

사인 코사인 변환

Sin cos, tan 공식

사인 코사인 탄젠트 관계

사인, 코사인, 탄젠트

Sin 표

사인, 코사인, 탄젠트 공식

사인 코사인 탄젠트 변환

삼각함수 공식

사인 코사인 표 주제와 관련된 상위 126 이미지

비디오 사인 코사인 표 삼각함수의 값 쉽게 구하기

주제에 대한 관련 정보 사인 코사인 표

Leave a Comment Cancel reply