톱 400 코사인 법칙 증명 업데이트 53 일 전

by

제2 코사인법칙 증명

코사인법칙 다양한 증명

코사인법칙 증명 평면좌표

구면 코사인법칙

사인법칙 코사인법칙

사인법칙 코사인법칙 증명

제이코사인법칙

제 3 코사인법칙

주제에 대한 기사를 찾고 있습니까 “코사인 법칙 증명“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: 974 사진을 다운로드할 수 있는 최고의 웹사이트. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.

이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.

컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.

코사인 법칙 증명 주제와 관련된 상위 51 이미지

주제 코사인 법칙 증명 와 관련된 30 개의 이미지가 있습니다.

제 2 코사인 법칙 유도와 벡터의 유사성

제 2 코사인 법칙은 제 1 코사인 법칙으로 부터 유도할 수 있다. 자세한 증명은 여기서 더 친절하게 설명하고 있다.이렇게 두 벡터의 사이각을 구할 수 있으면 뭐가 좋냐고?벡터의 유사도를 두 벡터가 이루는 각도로 설명할 수 있다. 데이터 과학에서 clustering과

  • Image source: velog.io
  • Views: 22562
  • Publish date: 16 minute ago
  • Downloads: 69865
  • Likes: 512
  • Dislikes: 2
제 2 코사인 법칙 유도와 벡터의 유사성
제 2 코사인 법칙 유도와 벡터의 유사성

데이터 과학에서 clustering과 classification와 같은 기술은 근본적으로 벡터간의 유사도를 기반으로 이론이 전개된다.

표본분포와 표집분포 (Sampling distribution vs. Sample distribution)

두 벡터의 거리(norm 1, 2)를 통해서 유사도를 판단할 수도 있고,

코사인 법칙 증명

코사인 법칙(코사인 제 2법칙) 증명 증명 1) – 피타고라스 정리의 확장 (일반화) 증명 2) – 방멱정리를 이용한 증명

  • Image source: mathpeak.tistory.com
  • Views: 61742
  • Publish date: 10 hours ago
  • Downloads: 1972
  • Likes: 5422
  • Dislikes: 7
코사인 법칙 증명
코사인 법칙 증명

고2 11월 전국연합학력평가 수학 문제지, 답지 및 등급컷 (2014년~2022년)

고2 11월 전국연합학력평가 수학 문제지, 답지 및 등급컷 (2014년~2022년)

고2 11월 전국연합학력평가 수학 문제지, 답지 및 등급컷 (2014년~2022년)

삼각함수의 정의를 이용한 제2코사인 법칙 증명

proof of second law of cosines

  • Image source: freshrimpsushi.github.io
  • Views: 67801
  • Publish date: 24 hours ago
  • Downloads: 7316
  • Likes: 4298
  • Dislikes: 2
삼각함수의 정의를 이용한 제2코사인 법칙 증명
삼각함수의 정의를 이용한 제2코사인 법칙 증명

b^{2}+c^{2} &= (bc\cos\alpha + ab\cos\gamma) + (bc\cos\alpha + ac\cos\beta)

$\eqref{eq1}$, $\eqref{eq2}$, $\eqref{eq3}$을 묶어 제1 코사인 법칙이라 부르기도 한다.

\\ && \implies b^{2}&=bc\cos\alpha + ab\cos\gamma \nonumber

고2 수학 삼각함수 코사인법칙증명 : 네이버 포스트

[BY 동백수학학원수학과외] 고2 수학 삼각함수 코사인법칙증명사인법칙이나 코사인법칙을 증명해보고 삼…

  • Image source: m.post.naver.com
  • Views: 64234
  • Publish date: 13 hours ago
  • Downloads: 31155
  • Likes: 5172
  • Dislikes: 5
고2 수학 삼각함수 코사인법칙증명 : 네이버 포스트
고2 수학 삼각함수 코사인법칙증명 : 네이버 포스트

좋아요 한 사람 보러가기

이전화면으로 가기

이전화면으로 가기

삼각함수의 정의를 이용한 제2코사인 법칙 증명

proof of second law of cosines

  • Image source: freshrimpsushi.github.io
  • Views: 79090
  • Publish date: 16 minute ago
  • Downloads: 98313
  • Likes: 9031
  • Dislikes: 7
삼각함수의 정의를 이용한 제2코사인 법칙 증명
삼각함수의 정의를 이용한 제2코사인 법칙 증명

b^{2}+c^{2} &= (bc\cos\alpha + ab\cos\gamma) + (bc\cos\alpha + ac\cos\beta)

$\eqref{eq1}$, $\eqref{eq2}$, $\eqref{eq3}$을 묶어 제1 코사인 법칙이라 부르기도 한다.

\\ && \implies b^{2}&=bc\cos\alpha + ab\cos\gamma \nonumber

코사인 제 2 법칙 증명 원리 이해하기 : 네이버 블로그

코사인 제 2 법칙은 가장 활용영역이 넓은 고등학교 기하다 배워 두면 사용할 분야가 다양하다 그런데 코사…

  • Image source: m.blog.naver.com
  • Views: 87553
  • Publish date: 21 hours ago
  • Downloads: 35731
  • Likes: 3656
  • Dislikes: 4
코사인 제 2 법칙 증명 원리 이해하기 : 네이버 블로그
코사인 제 2 법칙 증명 원리 이해하기 : 네이버 블로그

합성함수 미분을 못하면 치환적분도 못하고 미적분을 제대로 할 수가 없고 수학이 재미가 없다 (이 글 끝에…

치환적분은 적분에서 가장 중요한 파트이다 너무나 많이 나오기 때문이다 치환적분은 합성함수의 역이다 B…

코사인 법칙 증명

코사인 법칙(코사인 제 2법칙) 증명 증명 1) – 피타고라스 정리의 확장 (일반화) 증명 2) – 방멱정리를 이용한 증명

  • Image source: mathpeak.tistory.com
  • Views: 29440
  • Publish date: 29 minute ago
  • Downloads: 36271
  • Likes: 660
  • Dislikes: 8
코사인 법칙 증명
코사인 법칙 증명

고2 11월 전국연합학력평가 수학 문제지, 답지 및 등급컷 (2014년~2022년)

고2 11월 전국연합학력평가 수학 문제지, 답지 및 등급컷 (2014년~2022년)

고2 11월 전국연합학력평가 수학 문제지, 답지 및 등급컷 (2014년~2022년)

수학10-나 1학년 2학기 Ⅳ.삼각함수 1. 사인법칙과 코사인법칙 (11/12) 삼각함수 수업계획 수업활동. – ppt download

차 례 도 입 학습문제 학습활동1 학습활동2 학습활동3 정 리 1. 피타고라스의 정리를 알아 봅시다. 차 례 도 입 1. 피타고라스의 정리를 알아 봅시다. 학습문제 2. 공부할 문제를 알아봅시다. 학습활동1 3. 코사인법칙을 유도해 봅시다. 학습활동2 4. 제2코사인법칙을 구해 봅시다. 학습활동3 5. 코사인법칙을 실 생활에 활용해 봅시다. 정 리 6. 공부한 내용을 정리해 봅시다.

  • Image source: slidesplayer.org
  • Views: 13841
  • Publish date: 3 hours ago
  • Downloads: 67751
  • Likes: 6357
  • Dislikes: 1
수학10-나 1학년 2학기 Ⅳ.삼각함수 1. 사인법칙과 코사인법칙 (11/12) 삼각함수 수업계획 수업활동. - Ppt Download
수학10-나 1학년 2학기 Ⅳ.삼각함수 1. 사인법칙과 코사인법칙 (11/12) 삼각함수 수업계획 수업활동. – Ppt Download

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

 과학  4 학년 2 학기  2. 동물의 암수 ( 4/5 ) 동물의 새끼와 어미. 수업활동 안내 동물의 어미와 새끼 이름 알아보기 1 새끼와 어미의 모습이 비슷한 동물 2 새끼와 어미의 모습이 다른 동물 3 정리하기 5 4 새끼와 어미를 짝지어 보는 놀이하기.

To make this website work, we log user data and share it with processors. To use this website, you must agree to our

수학 – 미적분2 – 삼각함수- 오누이

  • Image source: onuii.com
  • Views: 39503
  • Publish date: 5 minute ago
  • Downloads: 32721
  • Likes: 9123
  • Dislikes: 7
수학 - 미적분2 - 삼각함수- 오누이
수학 – 미적분2 – 삼각함수- 오누이

코로나와 입시가 겹쳐져서 무척 힘든 시기일텐데, 아프지마시고 꼭 목표로하시는 곳 합격하길 바랄게요~ 열공 🙂

좌표평면 상에서 길이를 합칠 때, 이 값이 양의 값인지, 음의 값인지 잘 확인해야합니다!

풀이는 사진에 자세히 적어두었습니다. 혹시 안보이는 부분 있으면 재질문방 이용해주세요! 😊

삼각함수 공식 총 정리!!(덧셈법칙, 제곱공식, 사인법칙, 제2코사인법칙, 덧셈법칙, 2배각법칙, 합성법칙 등 공식모음)

안녕하세요. 훈릴스입니다. 오늘은 삼각함수의 공식을 모두 한 번 정리해보는 시간을 가져보고자 합니다. 정말 기본중에 기본적인 공식들이니 꼭꼭 암기하셔야하는데요. 너무 급하게 외우시기 보다는 하루에 한 번씩 써보는 것도 좋은 공부법이라고 생각되네요. 1. 삼각함수란 무엇인가 삼각함수 sin, cos, tan는 반지름 길이가 1인 원을 가지고 정의를 하는데요. 원 위의 한 점을 P(x,y)라고 하면 위와 같이 sin, cos, tan를 나타낼 수 있는 것이죠. 이렇게 어려운 것을 왜 정의하느냐라고 의문을 가지고 계신 분들이 있으실 것으로 생각 되네요. 하지만, 기초 중에 기초인 삼각함수를 이용하면 "복잡한 식을 간단하게" 만들 수 있기 때문에 이용해요! 처음에는 외울 것도 많으니 어려움을 겪으시겠지만 하나하..

  • Image source: alive-earth.com
  • Views: 91140
  • Publish date: 3 hours ago
  • Downloads: 92419
  • Likes: 7691
  • Dislikes: 6
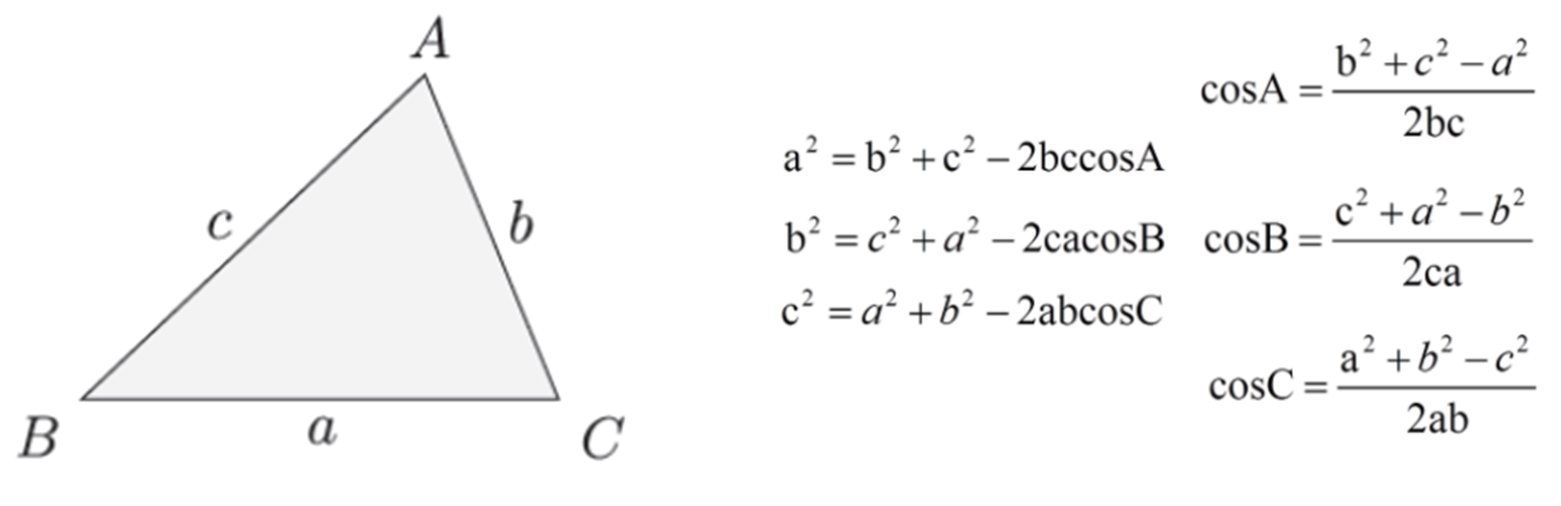
삼각함수 공식 총 정리!!(덧셈법칙, 제곱공식, 사인법칙, 제2코사인법칙, 덧셈법칙, 2배각법칙, 합성법칙 등 공식모음)
삼각함수 공식 총 정리!!(덧셈법칙, 제곱공식, 사인법칙, 제2코사인법칙, 덧셈법칙, 2배각법칙, 합성법칙 등 공식모음)

갑자기 무슨 말이냐라고 의문을 가지고 계신 분들이 계실 것으로 생각되네요! 위의 그림에서 삼각형의 각도에 따라서 삼각함수의 부호가 바뀌게 되는데요. 1사분면(0~90도)일 때는 sin,cos,tan 모두 양수죠! 2사분면(90~180도) 일때는 sin함수만 양수이고 cos과 tan는 음수에요. 3사분면(180~270도)에서는 tan만 양수이고, sin, cos는 음수에요. 4사분면(270~360도)에서는 cos만 양수이고 sin과 tan는 음수에요. 이렇게 각 사분면마다 양수인 부분만 따서 이름을 정한 것이 “얼싸탄코”라고 합니다!!

삼각함수 sin, cos, tan는 반지름 길이가 1인 원을 가지고 정의를 하는데요. 원 위의 한 점을 P(x,y)라고 하면 위와 같이 sin, cos, tan를 나타낼 수 있는 것이죠. 이렇게 어려운 것을 왜 정의하느냐라고 의문을 가지고 계신 분들이 있으실 것으로 생각 되네요. 하지만, 기초 중에 기초인 삼각함수를 이용하면 “복잡한 식을 간단하게” 만들 수 있기 때문에 이용해요! 처음에는 외울 것도 많으니 어려움을 겪으시겠지만 하나하나 살펴보면 쉽게 이해할 수 있을 것 같아요.

코사인 제 2법칙은 다음과 같아요. 어려워보이지만 사실은 간단해요!! 우리가 구하고자하는 변의 제곱은 다른 변의 제곱의 합에서 다른 두변의 곱에 2를 곱하고 구하고자하는 변의 마주편 각의 Cos을 곱한 것과 같답니다! 말로 표현하자니 어렵지만, 열 번 정도 공책에 적어보시면 원리를 쉽게 익히실 수 있을 것 같아요!. 코사인 제 2법칙은 다양한 문제에 적용되기에 꼭 알고 계셔야합니다!!

[수학설명] 15개정 수학1 – 삼각함수 코사인법칙 : 네이버 블로그

[수학설명] 15개정 수학1 – 삼각함수 코사인법칙 코사인법칙 증명 오늘은 사인법칙에 이어서 코사인 법칙 …

  • Image source: m.blog.naver.com
  • Views: 39527
  • Publish date: 30 minute ago
  • Downloads: 15053
  • Likes: 6273
  • Dislikes: 10
수학설명] 15개정 수학1 - 삼각함수 코사인법칙 : 네이버 블로그
수학설명] 15개정 수학1 – 삼각함수 코사인법칙 : 네이버 블로그

수학+입시+교육. 연대 교육대학원 졸업. 일하며 틈틈히. 수학강의 입시상담. jjangting

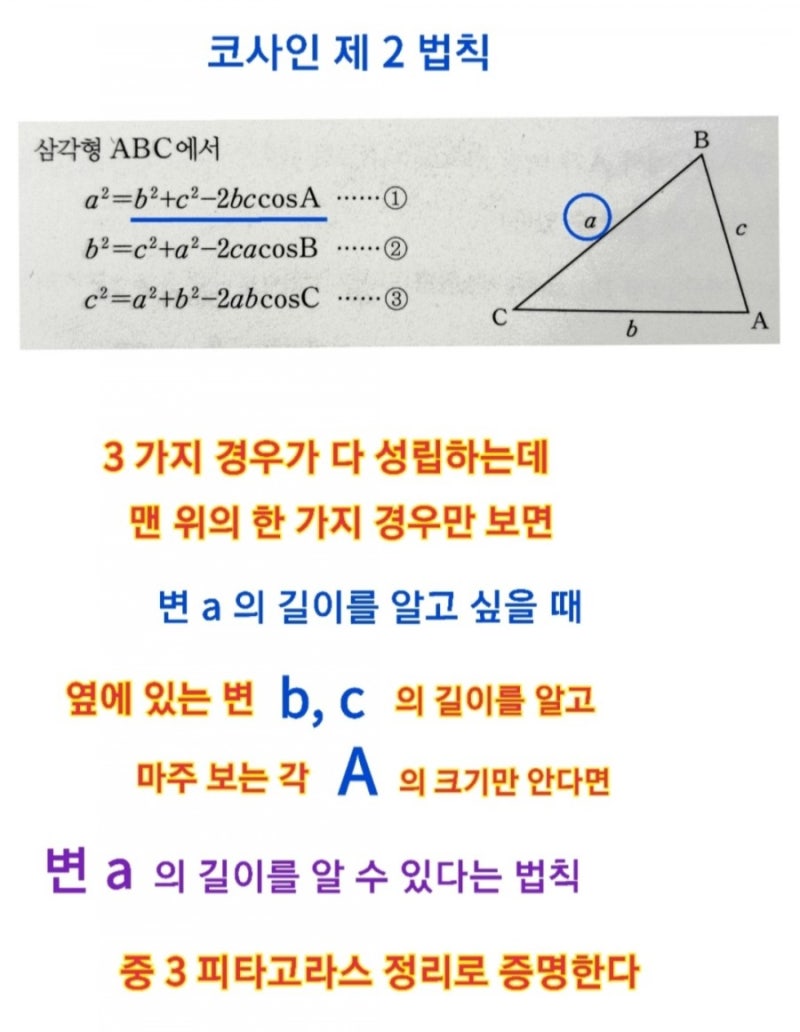
옛날에는 제2 코사인 법칙이라 불렸고 제1 코사인 법칙도 있었는데

코사인법칙으로 한 각의 크기 구하기 (동영상) | 코사인법칙 | Khan Academy

수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진 비영리기관입니다.

  • Image source: ko.khanacademy.org
  • Views: 67856
  • Publish date: 54 minute ago
  • Downloads: 103175
  • Likes: 5807
  • Dislikes: 10
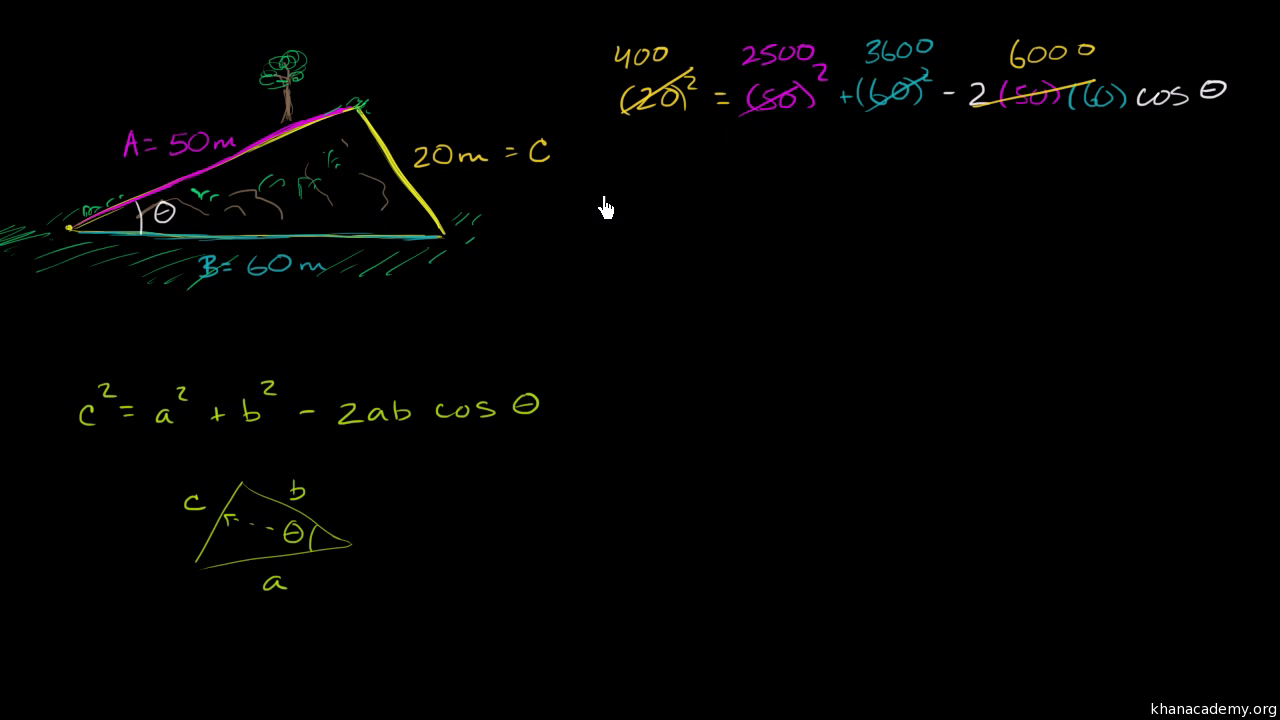
코사인법칙으로 한 각의 크기 구하기 (동영상) | 코사인법칙 | Khan Academy
코사인법칙으로 한 각의 크기 구하기 (동영상) | 코사인법칙 | Khan Academy

이 변이 A가 될 수 있습니다 이 각과 관련해서 우리가 하려는 것은 여기 있는 이 작은 언덕에서 세타의 크기를 찾으려고 합니다 이것이 세타라면 C는 어디가 될까요? C는 여기 20미터가 됩니다 그리고 A와 B는 이 두변 중에 하나 씩 이름을 씁니다 A를 50미터이고 B는 60미터입니다 이제 코사인법칙을 적용해 봅시다 코사인법칙은 20의 제곱은 A의 제곱과 같으므로 A의제곱에 50제곱을 쓰고 더하기 B제곱은 60제곱을 대입하고 2곱하기 AB를 빼면 2와 50과 60을 곱하고 cos세타를 곱합니다 모든 숫자들이 주어졌기 때문에 여기까지는 잘 되고 있습니다 단지 여기 세타만 모릅니다 여기 세타가 있습니다 이제 세타를 찾아 봅시다 20의 제곱은 400이고 50의 제곱은 2,500이고 60의 제곱은 3,600입니다 그리고 50 곱하기 자, 50의 2배는 100이고 여기에 60을 곱하면

알아내는 것입니다 바닥에 비례하는 실제 기울기는 얼마일까요? 다른 방법으로 생각하면 여기에 이 각 세타는 얼마일까요? 잠시 비디오를 멈추고 생각해 보세요 비슷한 경우가 있었습니다 여러분은 삼각형의 세변을 압니다 그리고 이 각의 크기를 알아내려고 합니다 내 머리 속에 떠오른 것은 코사인법칙을 사용하는 겁니다 여기 있는 삼각형에 코사인법칙을 적용하기 전에 코사인법칙을 한 번 써 봅시다 코사인법칙은 C의 제곱은 A의 제곱과 B의 제곱의 합에 2AB와 코사인 세타를 곱한 후 뺀 것과 같습니다 A, B 와 C가 무엇인지 짚어보고 간다면 C는 각 세타의 대변입니다 여기에 임의의 삼각형을 하나 그리고 이 각을 세타라고 하면 각 세타가 C를 결정하고 A와 B는 어느 변에 붙여도 상관없습니다 A는 이 변이고 B는 이 변이라고 할 수 있고 또는 그 반대로 붙여도 됩니다 여기서 보듯이,

6,000으로 나누어보겠습니다 그러면 양변을 바꿔봅시다 cos세타는 자, 분자와 분모를 마이너스 100으로 나누어 봅니다 그러면 분자 분모 둘다 플러스가 됩니다 cos세타는 57/60입니다 더 간단히 해보면 3으로 57을 나누면 19가 되겠죠? 예, 그래서 실제로 약분하면 19/20이 됩니다 우리가 실제로 약분을 할 필요는 없습니다 곧 계산기를 사용할 예정이니까요 좀 더 쉽게 계산하기 위해 자, 57을 3으로 나누면 19가 됩니다 이제는 양변을 cos의 역수로 나눌 수 있습니다 세타는 cos의 역수 또는 역cos과

[수학] 삼각함수 기초 – 1

삼각함수의 여러 기본 개념 작성과 공식들 유도해보기

  • Image source: velog.io
  • Views: 37883
  • Publish date: 21 hours ago
  • Downloads: 99927
  • Likes: 7909
  • Dislikes: 9
수학] 삼각함수 기초 - 1
수학] 삼각함수 기초 – 1

Computer vision 역시 수학적인 접근이 가능하지만, 공학적인 요소가 강하지만 Computer Graphics는 순수 수학적인 요소가 꽤 강하다고 생각한다.

그리고 Computer Graphics 의 Transform, Rotation, Scaling 이런 것들을 보면 전부 수학식, 특히 Matrix를 사용한다.

최적화 문제 해결 부터가 일단 테일러 급수(Taylor Series)를 사용하는 Gradient Descent 방식을 사용하기도 하고,

제2코사인법칙 공식 및 유도과정

제2코사인법칙이란? 임의의 삼각형이 주어졌을 때, 제1코사인법칙과 제2코사인법칙이 성립된다. 다음과 같은 삼각형이 주어졌을 때 다음과 같은 식이 성립한다. 위의 식을 제2코사인법칙이라고 한다. 상당히 많이 쓰이는 공식이며 식을 변형해서 많이 쓰기도 한다.↓ 공식 유도하기 제2코사인법칙은 모든 삼각형에서 증명이 가능하다. △ABC의 꼭지점 B에서 밑변 또는 그 연장선 위에 내린 수선의 발을 D, 선분BD=h, 선분AD=x라고 두자. 1. 예각삼각형의 경우 2. 둔각삼각형의 경우 3. 직각삼각형의 경우 똑같은 방법으로 b, c 꼴로도 정리할 수 있으니, 위의 증명과정을 참고하여 b, c도 직접 공식을 유도하면서 이해하며 암기하도록 하자. 함께 읽기 제1코사인법칙 및 유도과정에 대하여 알아보자 제1코사인법칙 ..

  • Image source: houseofj.tistory.com
  • Views: 100226
  • Publish date: 46 minute ago
  • Downloads: 30297
  • Likes: 3819
  • Dislikes: 3
제2코사인법칙 공식 및 유도과정
제2코사인법칙 공식 및 유도과정

제2코사인법칙은 모든 삼각형에서 증명이 가능하다. △ABC의 꼭지점 B에서 밑변 또는 그 연장선 위에 내린 수선의 발을 D, 선분BD=h, 선분AD=x라고 두자.

똑같은 방법으로 b, c 꼴로도 정리할 수 있으니, 위의 증명과정을 참고하여 b, c도 직접 공식을 유도하면서 이해하며 암기하도록 하자.

위의 식을 제2코사인법칙이라고 한다. 상당히 많이 쓰이는 공식이며 식을 변형해서 많이 쓰기도 한다.↓

비디오 코사인 법칙 증명 코사인 법칙

  • Source: Youtube
  • Views: 74621
  • Date: 23 minute ago
  • Download: 28460
  • Likes: 967
  • Dislikes: 7

주제에 대한 관련 정보 코사인 법칙 증명

Bing에서 코사인 법칙 증명 주제에 대한 최신 정보를 볼 수 있습니다.

제2 코사인법칙 증명

코사인법칙 다양한 증명

코사인법칙 증명 평면좌표

구면 코사인법칙

사인법칙 코사인법칙

사인법칙 코사인법칙 증명

제이코사인법칙

제 3 코사인법칙

주제에 대한 기사 보기를 마쳤습니다 코사인 법칙 증명. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.

제2 코사인법칙 증명

코사인법칙 다양한 증명

코사인법칙 증명 평면좌표

구면 코사인법칙

사인법칙 코사인법칙

사인법칙 코사인법칙 증명

제이코사인법칙

제 3 코사인법칙

Leave a Comment