톱 407 지수 함수 로그 함수 실생활 활용 새로운 업데이트 204 시간 전

by

로그함수 실생활 사례

지수함수 사회 현상

지수함수 실생활 활용 사례

로그함수 실생활 활용 문제

지수함수 실생활 경제

지수함수 실생활 활용 문제

컴퓨터 지수함수 활용

고2 수학 실생활 활용 사례

주제에 대한 기사를 찾고 있습니까 “지수 함수 로그 함수 실생활 활용“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: c2.castu.org/blog. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.

이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.

컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.

지수 함수 로그 함수 실생활 활용 주제와 관련된 상위 136 이미지

주제 지수 함수 로그 함수 실생활 활용 와 관련된 33 개의 이미지가 있습니다.

PPT – 지수함수와 로그함수 이야기 – 뉴 턴 – PowerPoint Presentation – ID:5583561

지수함수와 로그함수 이야기 – 뉴 턴 -. 한광고등학교 1 학년 8 반 32 번 최 우 년. 차 례. 뉴턴은 누구일까 ?? 뉴턴이 들려주는 지수함수와 로그함수 이야기 지수함수란 … 로그함수란 … 느낀점. Isaac Newton.

  • Image source: www.slideserve.com
  • Views: 98814
  • Publish date: 5 hours ago
  • Downloads: 19367
  • Likes: 4045
  • Dislikes: 7
Ppt - 지수함수와 로그함수 이야기 - 뉴 턴 - Powerpoint Presentation - Id:5583561
Ppt – 지수함수와 로그함수 이야기 – 뉴 턴 – Powerpoint Presentation – Id:5583561

나타내기 때문에 똑같은 지진이라도 지역에 따라 다르다. 따라서 지진을 분류할 때는 지진 자체의 크기를 어떤 척도에 따라 정량적으로 나타낼 필요가 있다. 이를 위해 현재 보편적으로 이용하는 방법이 1935년 리히터가 개발한 척도인 ‘규모’(magnitude)다. 지진의 규모는 진원지에서 1백km 떨어진 지점에서 지진계로 측정한 지진파의 최대 진폭에 따라 결정되는데, 지진파의 최대 진폭은 지진에 따라 대단히 큰 차이를 보인다. 이런 차이를 알기 쉽게 축소해 나타낸 것이 로그다. 지진파의 최대 진폭이 A미크론(1미크론=1천분의 1mm)인 지진의 규모 M은 상용 로그를 이용해 M log10 A(=log A)으로 정한다.그러므로 지진의 최대 진폭이 10배씩 커질 때마다 지진의 규모는 1.0씩 증가한다( log 1=0, log 10=1, log 102=2, … log 10n=n). 그리고 지진의 규모(M)와 지진에 의해 발생하는 에너지(E) 사이에는 log E=11.4+1.5M라는 관계가 성립한다. 지진 규모의 값이 1 증가하면 에너지는 약 32배로 증가한다는 것을 의미한다. • 101.5 ≒ 31.6227 ≒ 32

일찍부터 역학 문제, 특히 중력 문제에 대해서는 광학과 함께 큰 관심을 가지고 있었으며, 지구의 중력이 달의 궤도에까지 미친다고 생각하여 이것과 행성의 운동(이것을 지배하는 케플러법칙)과의 관련을 고찰한 것은 울즈소프 체류 때 이루졌다고 한다. 1687년 이 성과를 포함한 대저서 《자연철학의 수학적 원리(프린키피아) 》가 출판되었으며, 이로써 이론물리학의 기초가 쌓이고 뉴턴역학의 체계가 세워졌다.3부로 된 이 라틴어 저서는 간단한 유율법의 설명에서 시작하여 역학의 원리, 인력의 법칙과 그 응용, 유체의 문제, 태양행성의 운동에서 조석의 이론 등에 이르기까지 계통적으로 논술되어 있다. 또 방정식론 등의 대수학 분야의 여러 업적은 《Arithmetica universalis sive de compositione et resolutione arithmetica liber》(1707)로 간행되었다.  근대과학 성립의 최고의 공로자이며, 그가 주장한 ‘자연은 일정한 법칙에 따라 운동하는 복잡하고 거대한 기계’라고 하는 역학적 자연관은 18세기 계몽사상의 발전에 지대한 영향을 주었다.

• 잉글랜드 동부 링컨셔의 울즈소프에서 태어났다. 아버지는 그의 출생 전에 사망하였고, 어머니는 그가 3세 때 재혼하는 등 불운한 소년시절을 보냈다.수학에서 미적분법 창시, 물리학에서 뉴턴역학의 체계 확립, 이것에 표시된 수학적 방법 등은 자연과학의 모범이 되었고, 사상면에서도 역학적 자연관은 후세에 커다란 영향을 끼쳤다. 1661년 케임브리지대학교 트리니티칼리지에 입학, 수학자 I.배로의 지도를 받아 케플러의 《굴절광학》, 데카르트의 《해석기하학》, 월리스의 《무한의 산수》 등을 탐독하였으며, 1664년 학사학위를 얻었다. 1664~1666년 페스트가 크게 유행하자 대학이 일시 폐쇄되어 뉴턴도 고향으로 돌아와 대부분의 시간을 사색과 실험으로 보냈다. 그의 위대한 업적의 대부분은 이때 싹트게 된 것이라고 하며, 사과의 일화도 이때 있었던 일이다. 1667년 재개된 대학에 돌아와 이 대학의 펠로(특별연구원)가 되고 이듬해에는 메이저펠로(전임특별연구원)가 됨과 동시에 석사학위를 받았다. 1669년 I.배로의 뒤를 이어 루카스교수직에 부임하였다.

수 1 실생활 활용 사례 | ticket.hydeparkwinterwonderland.com

수 1 실생활 활용 사례, 롤 문화재 지킴이, 마디 사랑 병원

  • Image source: ticket.hydeparkwinterwonderland.com
  • Views: 31982
  • Publish date: 9 hours ago
  • Downloads: 96067
  • Likes: 1039
  • Dislikes: 1
수 1 실생활 활용 사례 | Ticket.Hydeparkwinterwonderland.Com
수 1 실생활 활용 사례 | Ticket.Hydeparkwinterwonderland.Com

또한 역사, 다양한 젖소 비키니 및 추세, 무역 개요, 수학 1 실생활 사례 젖소 비키니, 무역 및 시장 경쟁자와 같은 중요한 시장 자격 증명을 제공합니다. . 만약 음향 관련 기술을 다루는 엔지니어가 되고 싶다면 삼각함수와 친해져야 할 필요가 있습니다. 1892년 미국의 농부였던 페인타 부부가 발명한 이후로 이 병마개의 모양이나 톱니수는 한번도 바뀌지 않았다고 한다.

이 사실을 깨닫고 주의를 둘러본다면 하루에도 여러번 삼각함수와 마주칠지도 모릅니다. 그렇게 되면 아까운 종이와 펄프를 낭비하게 된다. 아시는 것이 있으시다면 제발 최대한 많이 알려주세여. 활용된지식: 계산 알고리즘 코딩 방법 암호화 여행 계획하기 여행을 간다는 것은 일상을 벗어나는 신선한 경험입니다.

하지만 전자계산기 사용 논란은 지금 시점에선 숲이 아니라 나무만 쳐다보고 이야기하는 셈이다. 그 만큼 수학은 어렵고 힘든 과목을 대표한다. 정확하게 말하면 동일한 공간의 방을 만드는데 정육각형에 비해 두배의 재료가 든다. 이런 스마트폰의 보급이나 판매량 역시 지수함수를 통해 예측해볼 수 있습니다.

지수로그 실생활에의 활용|샘토링 수학(samtoring)

지수로그 실생활에의 활용|샘토링 수학(samtoring)

  • Image source: samtoring.com
  • Views: 89940
  • Publish date: 11 hours ago
  • Downloads: 78423
  • Likes: 7770
  • Dislikes: 3
지수로그 실생활에의 활용|샘토링 수학(Samtoring)
지수로그 실생활에의 활용|샘토링 수학(Samtoring)

이 문제에 사용된 공식은 실제로 존재하는 건가요?존재한다면 공식의 명칭을 알고싶습니다

Ctrl+Shift+F : 문제 통합검색 창으로 포커스 이동

통신판매업신고 제2015-서울마포-1618 호 |

PPT – 지수함수와 로그함수 이야기 – 뉴 턴 – PowerPoint Presentation – ID:5583561

지수함수와 로그함수 이야기 – 뉴 턴 -. 한광고등학교 1 학년 8 반 32 번 최 우 년. 차 례. 뉴턴은 누구일까 ?? 뉴턴이 들려주는 지수함수와 로그함수 이야기 지수함수란 … 로그함수란 … 느낀점. Isaac Newton.

  • Image source: www.slideserve.com
  • Views: 9290
  • Publish date: 23 minute ago
  • Downloads: 70129
  • Likes: 7745
  • Dislikes: 6
Ppt - 지수함수와 로그함수 이야기 - 뉴 턴 - Powerpoint Presentation - Id:5583561
Ppt – 지수함수와 로그함수 이야기 – 뉴 턴 – Powerpoint Presentation – Id:5583561

나타내기 때문에 똑같은 지진이라도 지역에 따라 다르다. 따라서 지진을 분류할 때는 지진 자체의 크기를 어떤 척도에 따라 정량적으로 나타낼 필요가 있다. 이를 위해 현재 보편적으로 이용하는 방법이 1935년 리히터가 개발한 척도인 ‘규모’(magnitude)다. 지진의 규모는 진원지에서 1백km 떨어진 지점에서 지진계로 측정한 지진파의 최대 진폭에 따라 결정되는데, 지진파의 최대 진폭은 지진에 따라 대단히 큰 차이를 보인다. 이런 차이를 알기 쉽게 축소해 나타낸 것이 로그다. 지진파의 최대 진폭이 A미크론(1미크론=1천분의 1mm)인 지진의 규모 M은 상용 로그를 이용해 M log10 A(=log A)으로 정한다.그러므로 지진의 최대 진폭이 10배씩 커질 때마다 지진의 규모는 1.0씩 증가한다( log 1=0, log 10=1, log 102=2, … log 10n=n). 그리고 지진의 규모(M)와 지진에 의해 발생하는 에너지(E) 사이에는 log E=11.4+1.5M라는 관계가 성립한다. 지진 규모의 값이 1 증가하면 에너지는 약 32배로 증가한다는 것을 의미한다. • 101.5 ≒ 31.6227 ≒ 32

일찍부터 역학 문제, 특히 중력 문제에 대해서는 광학과 함께 큰 관심을 가지고 있었으며, 지구의 중력이 달의 궤도에까지 미친다고 생각하여 이것과 행성의 운동(이것을 지배하는 케플러법칙)과의 관련을 고찰한 것은 울즈소프 체류 때 이루졌다고 한다. 1687년 이 성과를 포함한 대저서 《자연철학의 수학적 원리(프린키피아) 》가 출판되었으며, 이로써 이론물리학의 기초가 쌓이고 뉴턴역학의 체계가 세워졌다.3부로 된 이 라틴어 저서는 간단한 유율법의 설명에서 시작하여 역학의 원리, 인력의 법칙과 그 응용, 유체의 문제, 태양행성의 운동에서 조석의 이론 등에 이르기까지 계통적으로 논술되어 있다. 또 방정식론 등의 대수학 분야의 여러 업적은 《Arithmetica universalis sive de compositione et resolutione arithmetica liber》(1707)로 간행되었다.  근대과학 성립의 최고의 공로자이며, 그가 주장한 ‘자연은 일정한 법칙에 따라 운동하는 복잡하고 거대한 기계’라고 하는 역학적 자연관은 18세기 계몽사상의 발전에 지대한 영향을 주었다.

• 잉글랜드 동부 링컨셔의 울즈소프에서 태어났다. 아버지는 그의 출생 전에 사망하였고, 어머니는 그가 3세 때 재혼하는 등 불운한 소년시절을 보냈다.수학에서 미적분법 창시, 물리학에서 뉴턴역학의 체계 확립, 이것에 표시된 수학적 방법 등은 자연과학의 모범이 되었고, 사상면에서도 역학적 자연관은 후세에 커다란 영향을 끼쳤다. 1661년 케임브리지대학교 트리니티칼리지에 입학, 수학자 I.배로의 지도를 받아 케플러의 《굴절광학》, 데카르트의 《해석기하학》, 월리스의 《무한의 산수》 등을 탐독하였으며, 1664년 학사학위를 얻었다. 1664~1666년 페스트가 크게 유행하자 대학이 일시 폐쇄되어 뉴턴도 고향으로 돌아와 대부분의 시간을 사색과 실험으로 보냈다. 그의 위대한 업적의 대부분은 이때 싹트게 된 것이라고 하며, 사과의 일화도 이때 있었던 일이다. 1667년 재개된 대학에 돌아와 이 대학의 펠로(특별연구원)가 되고 이듬해에는 메이저펠로(전임특별연구원)가 됨과 동시에 석사학위를 받았다. 1669년 I.배로의 뒤를 이어 루카스교수직에 부임하였다.

목적과 방향을 알려주는 수학 | 샘토링 수학(samtoring)

원격 수학 멘토링 시스템 | 샘토링 (samtoring.com)

  • Image source: samtoring.com
  • Views: 70229
  • Publish date: 50 minute ago
  • Downloads: 74983
  • Likes: 709
  • Dislikes: 10
목적과 방향을 알려주는 수학 | 샘토링 수학(Samtoring)
목적과 방향을 알려주는 수학 | 샘토링 수학(Samtoring)

Ctrl+Shift+F : 문제 통합검색 창으로 포커스 이동

이메일을 입력해 주시면 완료 후 이메일을 보내드리겠습니다.

통신판매업신고 제2015-서울마포-1618 호 |

PPT – 지수함수와 로그함수 이야기 – 뉴 턴 – PowerPoint Presentation – ID:5583561

지수함수와 로그함수 이야기 – 뉴 턴 -. 한광고등학교 1 학년 8 반 32 번 최 우 년. 차 례. 뉴턴은 누구일까 ?? 뉴턴이 들려주는 지수함수와 로그함수 이야기 지수함수란 … 로그함수란 … 느낀점. Isaac Newton.

  • Image source: www.slideserve.com
  • Views: 1295
  • Publish date: 2 hours ago
  • Downloads: 58917
  • Likes: 7742
  • Dislikes: 7
Ppt - 지수함수와 로그함수 이야기 - 뉴 턴 - Powerpoint Presentation - Id:5583561
Ppt – 지수함수와 로그함수 이야기 – 뉴 턴 – Powerpoint Presentation – Id:5583561

나타내기 때문에 똑같은 지진이라도 지역에 따라 다르다. 따라서 지진을 분류할 때는 지진 자체의 크기를 어떤 척도에 따라 정량적으로 나타낼 필요가 있다. 이를 위해 현재 보편적으로 이용하는 방법이 1935년 리히터가 개발한 척도인 ‘규모’(magnitude)다. 지진의 규모는 진원지에서 1백km 떨어진 지점에서 지진계로 측정한 지진파의 최대 진폭에 따라 결정되는데, 지진파의 최대 진폭은 지진에 따라 대단히 큰 차이를 보인다. 이런 차이를 알기 쉽게 축소해 나타낸 것이 로그다. 지진파의 최대 진폭이 A미크론(1미크론=1천분의 1mm)인 지진의 규모 M은 상용 로그를 이용해 M log10 A(=log A)으로 정한다.그러므로 지진의 최대 진폭이 10배씩 커질 때마다 지진의 규모는 1.0씩 증가한다( log 1=0, log 10=1, log 102=2, … log 10n=n). 그리고 지진의 규모(M)와 지진에 의해 발생하는 에너지(E) 사이에는 log E=11.4+1.5M라는 관계가 성립한다. 지진 규모의 값이 1 증가하면 에너지는 약 32배로 증가한다는 것을 의미한다. • 101.5 ≒ 31.6227 ≒ 32

일찍부터 역학 문제, 특히 중력 문제에 대해서는 광학과 함께 큰 관심을 가지고 있었으며, 지구의 중력이 달의 궤도에까지 미친다고 생각하여 이것과 행성의 운동(이것을 지배하는 케플러법칙)과의 관련을 고찰한 것은 울즈소프 체류 때 이루졌다고 한다. 1687년 이 성과를 포함한 대저서 《자연철학의 수학적 원리(프린키피아) 》가 출판되었으며, 이로써 이론물리학의 기초가 쌓이고 뉴턴역학의 체계가 세워졌다.3부로 된 이 라틴어 저서는 간단한 유율법의 설명에서 시작하여 역학의 원리, 인력의 법칙과 그 응용, 유체의 문제, 태양행성의 운동에서 조석의 이론 등에 이르기까지 계통적으로 논술되어 있다. 또 방정식론 등의 대수학 분야의 여러 업적은 《Arithmetica universalis sive de compositione et resolutione arithmetica liber》(1707)로 간행되었다.  근대과학 성립의 최고의 공로자이며, 그가 주장한 ‘자연은 일정한 법칙에 따라 운동하는 복잡하고 거대한 기계’라고 하는 역학적 자연관은 18세기 계몽사상의 발전에 지대한 영향을 주었다.

• 잉글랜드 동부 링컨셔의 울즈소프에서 태어났다. 아버지는 그의 출생 전에 사망하였고, 어머니는 그가 3세 때 재혼하는 등 불운한 소년시절을 보냈다.수학에서 미적분법 창시, 물리학에서 뉴턴역학의 체계 확립, 이것에 표시된 수학적 방법 등은 자연과학의 모범이 되었고, 사상면에서도 역학적 자연관은 후세에 커다란 영향을 끼쳤다. 1661년 케임브리지대학교 트리니티칼리지에 입학, 수학자 I.배로의 지도를 받아 케플러의 《굴절광학》, 데카르트의 《해석기하학》, 월리스의 《무한의 산수》 등을 탐독하였으며, 1664년 학사학위를 얻었다. 1664~1666년 페스트가 크게 유행하자 대학이 일시 폐쇄되어 뉴턴도 고향으로 돌아와 대부분의 시간을 사색과 실험으로 보냈다. 그의 위대한 업적의 대부분은 이때 싹트게 된 것이라고 하며, 사과의 일화도 이때 있었던 일이다. 1667년 재개된 대학에 돌아와 이 대학의 펠로(특별연구원)가 되고 이듬해에는 메이저펠로(전임특별연구원)가 됨과 동시에 석사학위를 받았다. 1669년 I.배로의 뒤를 이어 루카스교수직에 부임하였다.

자이 미2 지수로그함수 – 오르비

자이 미2 지수로그함수 중에 이런 문제는 안풀어도 되죠??

  • Image source: orbi.kr
  • Views: 76294
  • Publish date: 48 minute ago
  • Downloads: 93760
  • Likes: 676
  • Dislikes: 6
자이 미2 지수로그함수 - 오르비
자이 미2 지수로그함수 – 오르비

<의대생 수학과외> 광주 조선대학교 의과대학 – 내신 / 수능 / 기초다지기 / 킬러문제 / 성적향상

육군보다 병장 3개월 더 길어서 그만큼 돈 더받은ㅋㅋㅋㅋ엌ㅋㅋㅋㅋ 개꿀~~~ㅋㅋㅋㅋㅋ 하 씨발ㅋㅋ

나이대는 일찍 풀린 친구들은 검사도 하고 사무관도 하고 회계법인도 들어가있고 한의사도 하고 그럼

지수, 로그 – 두 가지 방법으로 푸는 문제

일반적으로 지수를 맨 처음에 배울 땐, 밑이 서로 다른데 지수법칙을 이용하여 원하는 값을 구하는 문제들이 나옵니다. 이번엔 밑이 같은 경우를 해볼게요. 로그를 배우기 전에는 지수를 변형해서 풀어야 하기 때문에, 조금 어렵게 느껴질 수도 있어요. 로그를 배운 후라면 큰 고민없이 그냥 로그로 푸셔도 됩니다. 문제1 2017학년도 경찰대 기출 sol1) 지수로 풀기 구해야 하는 식의 밑이 3이죠. 그런데 우리가 문제 조건에서 주어진 숫자는 밑인 12와 5,4입니다. 이걸 갖고 3을 만들어보는게 바로 이 문제의 포인트죠. 여기서 12를 4로 나누면 3이 나옵니다. 이제 이걸 주어진 식에 대입하면 됩니다. sol2) 로그로 풀기 뭐.. 사실 밑이 같기 때문에 로그로 풀면 다 풀립니다. 둘 다 로그로 나타내주면, ..

  • Image source: ladyang86.tistory.com
  • Views: 100313
  • Publish date: 23 hours ago
  • Downloads: 63813
  • Likes: 1004
  • Dislikes: 8
지수, 로그 - 두 가지 방법으로 푸는 문제
지수, 로그 – 두 가지 방법으로 푸는 문제

[수열] 등차수열의 합으로부터 등차수열의 일반항 빨리 구하는 방법

5종 교과서 수학적 귀납법 문제 모음 (2015 개정기준)

5종 교과서 수학적 귀납법 문제 모음 (2015 개정기준)

PPT – 지수함수와 로그함수 이야기 – 뉴 턴 – PowerPoint Presentation – ID:5583561

지수함수와 로그함수 이야기 – 뉴 턴 -. 한광고등학교 1 학년 8 반 32 번 최 우 년. 차 례. 뉴턴은 누구일까 ?? 뉴턴이 들려주는 지수함수와 로그함수 이야기 지수함수란 … 로그함수란 … 느낀점. Isaac Newton.

  • Image source: www.slideserve.com
  • Views: 27666
  • Publish date: 47 minute ago
  • Downloads: 66324
  • Likes: 1904
  • Dislikes: 5
Ppt - 지수함수와 로그함수 이야기 - 뉴 턴 - Powerpoint Presentation - Id:5583561
Ppt – 지수함수와 로그함수 이야기 – 뉴 턴 – Powerpoint Presentation – Id:5583561

나타내기 때문에 똑같은 지진이라도 지역에 따라 다르다. 따라서 지진을 분류할 때는 지진 자체의 크기를 어떤 척도에 따라 정량적으로 나타낼 필요가 있다. 이를 위해 현재 보편적으로 이용하는 방법이 1935년 리히터가 개발한 척도인 ‘규모’(magnitude)다. 지진의 규모는 진원지에서 1백km 떨어진 지점에서 지진계로 측정한 지진파의 최대 진폭에 따라 결정되는데, 지진파의 최대 진폭은 지진에 따라 대단히 큰 차이를 보인다. 이런 차이를 알기 쉽게 축소해 나타낸 것이 로그다. 지진파의 최대 진폭이 A미크론(1미크론=1천분의 1mm)인 지진의 규모 M은 상용 로그를 이용해 M log10 A(=log A)으로 정한다.그러므로 지진의 최대 진폭이 10배씩 커질 때마다 지진의 규모는 1.0씩 증가한다( log 1=0, log 10=1, log 102=2, … log 10n=n). 그리고 지진의 규모(M)와 지진에 의해 발생하는 에너지(E) 사이에는 log E=11.4+1.5M라는 관계가 성립한다. 지진 규모의 값이 1 증가하면 에너지는 약 32배로 증가한다는 것을 의미한다. • 101.5 ≒ 31.6227 ≒ 32

일찍부터 역학 문제, 특히 중력 문제에 대해서는 광학과 함께 큰 관심을 가지고 있었으며, 지구의 중력이 달의 궤도에까지 미친다고 생각하여 이것과 행성의 운동(이것을 지배하는 케플러법칙)과의 관련을 고찰한 것은 울즈소프 체류 때 이루졌다고 한다. 1687년 이 성과를 포함한 대저서 《자연철학의 수학적 원리(프린키피아) 》가 출판되었으며, 이로써 이론물리학의 기초가 쌓이고 뉴턴역학의 체계가 세워졌다.3부로 된 이 라틴어 저서는 간단한 유율법의 설명에서 시작하여 역학의 원리, 인력의 법칙과 그 응용, 유체의 문제, 태양행성의 운동에서 조석의 이론 등에 이르기까지 계통적으로 논술되어 있다. 또 방정식론 등의 대수학 분야의 여러 업적은 《Arithmetica universalis sive de compositione et resolutione arithmetica liber》(1707)로 간행되었다.  근대과학 성립의 최고의 공로자이며, 그가 주장한 ‘자연은 일정한 법칙에 따라 운동하는 복잡하고 거대한 기계’라고 하는 역학적 자연관은 18세기 계몽사상의 발전에 지대한 영향을 주었다.

• 잉글랜드 동부 링컨셔의 울즈소프에서 태어났다. 아버지는 그의 출생 전에 사망하였고, 어머니는 그가 3세 때 재혼하는 등 불운한 소년시절을 보냈다.수학에서 미적분법 창시, 물리학에서 뉴턴역학의 체계 확립, 이것에 표시된 수학적 방법 등은 자연과학의 모범이 되었고, 사상면에서도 역학적 자연관은 후세에 커다란 영향을 끼쳤다. 1661년 케임브리지대학교 트리니티칼리지에 입학, 수학자 I.배로의 지도를 받아 케플러의 《굴절광학》, 데카르트의 《해석기하학》, 월리스의 《무한의 산수》 등을 탐독하였으며, 1664년 학사학위를 얻었다. 1664~1666년 페스트가 크게 유행하자 대학이 일시 폐쇄되어 뉴턴도 고향으로 돌아와 대부분의 시간을 사색과 실험으로 보냈다. 그의 위대한 업적의 대부분은 이때 싹트게 된 것이라고 하며, 사과의 일화도 이때 있었던 일이다. 1667년 재개된 대학에 돌아와 이 대학의 펠로(특별연구원)가 되고 이듬해에는 메이저펠로(전임특별연구원)가 됨과 동시에 석사학위를 받았다. 1669년 I.배로의 뒤를 이어 루카스교수직에 부임하였다.

목적과 방향을 알려주는 수학 | 샘토링 수학(samtoring)

원격 수학 멘토링 시스템 | 샘토링 (samtoring.com)

  • Image source: samtoring.com
  • Views: 67946
  • Publish date: 7 hours ago
  • Downloads: 1913
  • Likes: 6776
  • Dislikes: 1
목적과 방향을 알려주는 수학 | 샘토링 수학(Samtoring)
목적과 방향을 알려주는 수학 | 샘토링 수학(Samtoring)

Ctrl+Shift+F : 문제 통합검색 창으로 포커스 이동

이메일을 입력해 주시면 완료 후 이메일을 보내드리겠습니다.

| 계산복잡도 :

목적과 방향을 알려주는 수학 | 샘토링 수학(samtoring)

원격 수학 멘토링 시스템 | 샘토링 (samtoring.com)

  • Image source: samtoring.com
  • Views: 17645
  • Publish date: 45 minute ago
  • Downloads: 64299
  • Likes: 5254
  • Dislikes: 7
목적과 방향을 알려주는 수학 | 샘토링 수학(Samtoring)
목적과 방향을 알려주는 수학 | 샘토링 수학(Samtoring)

Ctrl+Shift+F : 문제 통합검색 창으로 포커스 이동

이메일을 입력해 주시면 완료 후 이메일을 보내드리겠습니다.

육군사관학교/이과/수능/모평/사설/사용자등록/수학 가형

±¹Á¦½Å¹®

  • Image source: www.kookje.co.kr
  • Views: 78665
  • Publish date: 52 minute ago
  • Downloads: 56221
  • Likes: 4369
  • Dislikes: 5
국제신문
국제신문

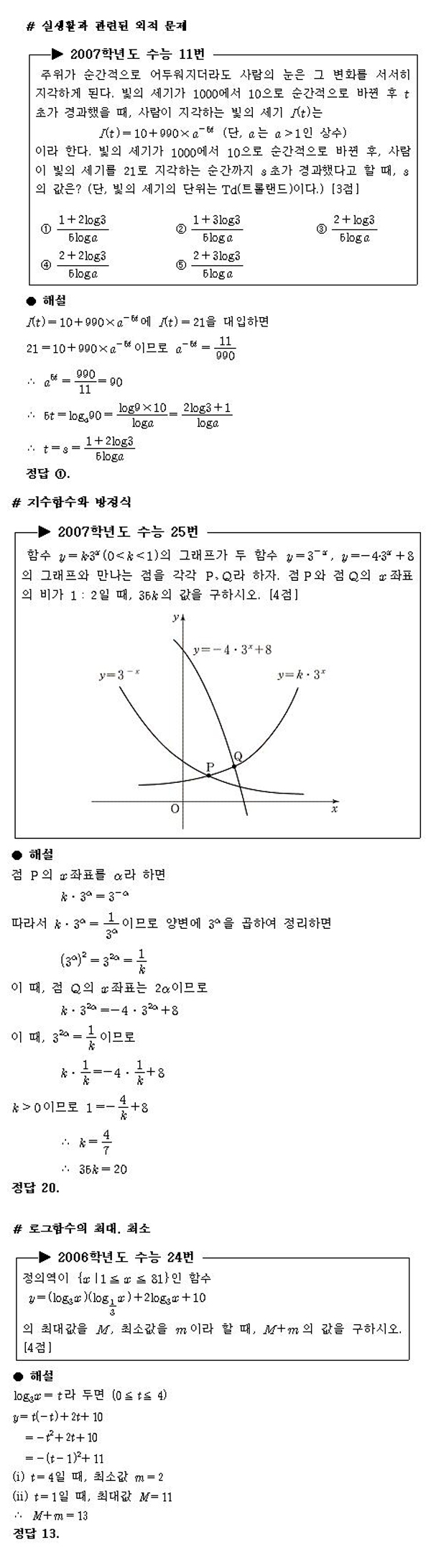
Áö¼öÇÔ¼ö¿Í ·Î±×ÇÔ¼ö´Â Áõ°¡ ¶Ç´Â °¨¼ÒÇÔ¼ö°¡ µÊÀ» ±×·¡ÇÁ¿Í °ü·ÃÁö¾î¼­ ÀÌÇØÇϵµ·Ï ÇÑ´Ù. Áö¼ö¡¤·Î±× ¹æÁ¤½ÄÀ̳ª ºÎµî½ÄÀ» Ç® ¶§´Â ¹Ø°ú Áø¼ö Á¶°ÇÀ» ¹Ýµå½Ã È®ÀÎÇÏ°í, ƯÈ÷ ºÎµî½ÄÀ» Ç® ¶§´Â ºÎµîÈ£°¡ º¯ÇÏ´ÂÁö¸¦ Àß ÆľÇÇÏÀÚ. ¶Ç ÀÌ ´Ü¿ø¿¡¼­´Â 10-³ªÀÇ µµÇüÀÇ ÆòÇà, ´ëĪÀ̵¿À̳ª »ï°¢ÇÔ¼ö, ¼ö¿­°ú À¶ÇÕµÈ ¹®Á¦°¡ ÃâÁ¦µÉ °¡´É¼ºÀÌ ³ôÀ¸¹Ç·Î 10-³ªÀÇ ³»¿ëµµ ¹Ýµå½Ã ¼÷ÁöÇÏ°í ÀÖ¾î¾ß ÇÑ´Ù. Áö¼öÇÔ¼ö¿Í ·Î±×ÇÔ¼ö°¡ ¿ªÇÔ¼öÀÇ °ü°è¸¦ °¡Áö¹Ç·Î Á÷¼± y=x¿¡ ´ëÇÏ¿© ¼­·Î ´ëĪÀÓÀ» ÀÌÇØ, ÁÖ¾îÁø ÇÔ¼öÀÇ ¿ªÇÔ¼ö¸¦ ±¸ÇÒ ¼ö ÀÖµµ·Ï ÇØ¾ß ÇÑ´Ù.

±¹Á¦½Å¹®Àº ºÎ»êÁ¾·ÎÇпø°ú ÇÔ²² 1994~2007Çг⵵ ´ëÇмöÇдɷ½ÃÇè(¼ö´É) ±âÃâ¹®Á¦¸¦ ½Éµµ ÀÖ°Ô ºÐ¼®, 14³â°£ ÃâÁ¦ °æÇâ°ú ÀÌ¿¡ µû¸¥ 2008Çг⵵ ¼ö´É ´ëºñ¹ýÀ» ¼Ò°³ÇÏ´Â ‘¼ö´É 14³â ±âÃâ¹®Á¦ ºÐ¼®’ ½Ã¸®Á ÃÑ 28ȸ¿¡ °ÉÃÄ ½Æ´Â´Ù. À̹ø 17ȸ¿¡¼­´Â ¼ö¸®¿µ¿ª Áß ‘Áö¼ö¿Í ·Î±×’¿Í ‘Áö¼ö¡¤·Î±×ÇÔ¼ö’¸¦ Á¤¸®Çß´Ù. Áö¸é¿¡ ½ÆÁö ¸øÇÑ ¹®Á¦´Â ±¹Á¦½Å¹® ÀÎÅÍ³Ý È¨ÆäÀÌÁö(www.kookje.co.kr)¿¡ °ÔÀçÇÑ´Ù.

ÁöÇ¥¿Í °¡¼ö¿¡ ´ëÇÑ ¿©·¯ ¹®Á¦¸¦ ÅëÇØ »ó¿ë·Î±×ÀÇ ÁöÇ¥¿Í °¡¼öÀÇ ¼ºÁúÀ» ¹¯´Â ¹®Á¦, Áö¼ö³ª »ó¿ë·Î±×ÀÇ ¼ºÁúÀ» ÀÌ¿ëÇØ ´Ù¾çÇÑ Çö»óÀ» ³ªÅ¸³»´Â ¿©·¯ °ø½ÄÀ» È°¿ëÇÑ ½Ç»ýÈ°°ú °ü·ÃµÈ ¿ÜÀû ¹®Á¦ µîÀº ¾î·Æ°Ô º¸¿©µµ ´ëºÎºÐ »õ·Î¿î Á¤ÀÇ°¡ ÁÖ¾îÁö°í, ÁÖ¾îÁø Á¶°ÇÀ» ´ëÀÔÇÏ¸é ½±°Ô ÇØ°áÇÒ ¼ö ÀÖ´Ù. µû¶ó¼­ ¹®Á¦¿¡¼­ ÁÖ¾îÁø Á¶°ÇÀ» ºüÁü¾øÀÌ ÀÌ¿ëÇß´ÂÁö¸¦ È®ÀÎÇÏ´Â ½À°üÀ» ±æ·¯¾ß ÇÑ´Ù.

지수/로그함수 그래프로 대소비교(ㄱㄴㄷ문제)

지수/로그함수 그래프 ㄱㄴㄷ 문제가 최근 다시 나오고 있죠. 그래프를 정확하게 그려서 추론하는 문제인데, 수능특강과 6,10월 모의고사에 모두 나온 문제라 수능보기 전에 정리하고 들어갑시다..! 아래 있는 문제들 열심히 풀어볼까요? 문제의 의도는 교점을 직접 구하라는 게 아닙니다. 1. 근처의 값들을 이용하여, 대소를 비교. 2. 평균변화율로 해석. 3. 대칭성을 적극 이용. 6월 21번 1.2.3번을 모두 사용하는 문제죠. 10월 21번 ㄴ이 가장 어려움. 왜냐하면 세제곱근2를 함수에 각각 넣어보면, 2의 -세제곱근2 승과 1/3을 비교해야하는데 밑이 달라 직접 비교가 어려움. 그래서 세제곱근2 < 2√2 < 3과 같이 중간에 2√2를 끼워서 비교해야 함. 이걸 어떻게 생각하지..? 숫자를 보아하니 다..

  • Image source: ladyang86.tistory.com
  • Views: 72021
  • Publish date: 14 hours ago
  • Downloads: 70569
  • Likes: 4913
  • Dislikes: 3
지수/로그함수 그래프로 대소비교(ㄱㄴㄷ문제)
지수/로그함수 그래프로 대소비교(ㄱㄴㄷ문제)

그래서 세제곱근2 < 2√2 < 3과 같이 중간에 2√2를 끼워서 비교해야 함.

2의 -세제곱근2 승과 1/3을 비교해야하는데 밑이 달라 직접 비교가 어려움.

[수열] 등차수열의 합으로부터 등차수열의 일반항 빨리 구하는 방법

비디오 지수 함수 로그 함수 실생활 활용 상용로그 실생활 활용문제 (요청강의입니다) / 15초 안에 식 세우는 방법

  • Source: Youtube
  • Views: 75789
  • Date: 16 hours ago
  • Download: 96262
  • Likes: 9978
  • Dislikes: 9

주제에 대한 관련 정보 지수 함수 로그 함수 실생활 활용

Bing에서 지수 함수 로그 함수 실생활 활용 주제에 대한 최신 정보를 볼 수 있습니다.

로그함수 실생활 사례

지수함수 사회 현상

지수함수 실생활 활용 사례

로그함수 실생활 활용 문제

지수함수 실생활 경제

지수함수 실생활 활용 문제

컴퓨터 지수함수 활용

고2 수학 실생활 활용 사례

주제에 대한 기사 보기를 마쳤습니다 지수 함수 로그 함수 실생활 활용. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.

로그함수 실생활 사례

지수함수 사회 현상

지수함수 실생활 활용 사례

로그함수 실생활 활용 문제

지수함수 실생활 경제

지수함수 실생활 활용 문제

컴퓨터 지수함수 활용

고2 수학 실생활 활용 사례

Leave a Comment