톱 713 리만 제타 함수 그래프 새로운 업데이트 199 시간 전

by

리만제타함수 계산

리만가설

리만 제타 함수 영점

리만제타함수 해석적확장

리만제타함수 양자역학

리만 제타 함수 자명한 근

리만가설 북한

제타함수 계산기

주제에 대한 기사를 찾고 있습니까 “리만 제타 함수 그래프“? 웹사이트에서 이 주제에 대한 전체 정보를 제공합니다 c2.castu.org 탐색에서: 292 사진을 다운로드할 수 있는 최고의 웹사이트. 바로 아래에서 이 주제에 대한 자세한 답변을 찾을 수 있습니다. 찾고 있는 주제를 더 잘 이해하려면 끝까지 읽으십시오.

이미지를 휴대폰에 다운로드하려면 이미지를 2초 동안 두 번 클릭한 다음 “이미지 다운로드” 다운로드를 선택하여 이미지를 다운로드할 수 있습니다.

컴퓨터에서 이미지를 다운로드하려면 이미지를 클릭한 다음 “다른 이름으로 이미지 저장”을 선택하여 다운로드할 수 있습니다.

리만 제타 함수 그래프 주제와 관련된 상위 144 이미지

주제 리만 제타 함수 그래프 와 관련된 42 개의 이미지가 있습니다.

  • Image source: namu.wiki
  • Views: 58307
  • Publish date: 22 minute ago
  • Downloads: 71207
  • Likes: 7474
  • Dislikes: 4
리만 가설 - 나무위키
리만 가설 – 나무위키

L-함수 – 위키백과, 우리 모두의 백과사전

  • Image source: ko.wikipedia.org
  • Views: 95897
  • Publish date: 28 minute ago
  • Downloads: 907
  • Likes: 2527
  • Dislikes: 6
L-함수 - 위키백과, 우리 모두의 백과사전
L-함수 – 위키백과, 우리 모두의 백과사전

O. Shanker (2006). “Random matrices, generalized zeta functions and self-similarity of zero distributions”. 《J. Phys. A: Math. Gen.》

가 해석적 관점에서 정확한 L-함수를 제공하는 방법으로 구축된다는 것이 명확해졌다. 즉 자기동형 사상과 관련되는 방식이어야 한다는 것이다. 일반적으로는 다수의 다른 연구 프로그램을 개념 수준에서 통합한다.

을 만든다. 이 오일러 곱이 복소 상반평면의 오른쪽 일부에서 수렴하는 것을 증명할 수 있는지 확인한다. 그리고 복소 평면의 나머지 영역에서도 해석적 확장을 통해 정의될 수 있는지 확인한다 (몇몇

Redirect

  • Image source: www.ibric.org
  • Views: 92147
  • Publish date: 23 hours ago
  • Downloads: 72301
  • Likes: 7779
  • Dislikes: 6
수학] 새로운 오일러 스타일 공식 > Bric” style=”width:100%”><figcaption>수학] 새로운 오일러 스타일 공식 > Bric</figcaption></figure> </div> <hr> <p>리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | YES24 블로그</p> <p><p>선생님이 1부터 100까지 더하는 문제를 냈는데 어린 가우스는 단번에 답을 말했다고 한다. 답은 바로 101*100/2=5050이다. 1부터 100까지 숫자를 한 줄로 늘어트려 놓았을 때, 차례대로 양끝의 숫자 두 개를 더하면 항상 101이다(1…</p> </p> <ul> <li><span>Image source: blog.yes24.com</span></li> <li><span>Views: 33176</span></li> <li><span>Publish date: 38 minute ago</span></li> <li><span>Downloads: 49938</span></li> <li><span>Likes: 688</span></li> <li><span>Dislikes: 8</span></li> </ul> <div> <figure><img decoding=
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | Yes24 블로그 – 내 삶의 쉼표

)을 이해하기 위해서는 소수정리를 비롯하여 조화수열, 로그함수, 미적분, 확률, 제타 함수, 복소평면 등의 수학지식을 알고 있어야 한다(알고 있어도 제대로 이해하는 사람은 드물다고 한다). 즉, 진입장벽이 높다. 제타 함수 하나만 해도 정말 특이하고 이해하기 어려운 함수이다. 이 제타 함수를 복소평면에 나타내고 자명하지 않는(허수인) 근들의 실수부가 1/2인 것을 구하는 것만 해도 많은 시간이 걸릴 것이다. 그렇기 때문에 수학에 관심이 있는 사람들만 리만 가설에 도전한다. 이렇게 난해한 리만 가설을 일반인들이 알기 쉽게 책으로 펴냈다는 것은 정말 대단한 것이다. 수학에 대한 전문적인 지식이 없는 일반인들은 이 책 한 권으로 리만 가설을 이해할 수 있다고 나는 말할 수 있다! 저자 더비셔는 리만 가설의 그 높은 진입장벽은 걸어서 넘을 정도로 낮춰줬다. 저자는 아직도 풀리지 않고 있는 리만 가설을 대중들에게 설명하고 혹시나 그 대중들이 관심을 가져서 리만 가설이 풀어지기를 기대한 것은 아닐까?

그 밖에 오일러(러시아의 표트르 대제에게 스카웃당한) 등의 수학자들과 관련된 흥미로운 이야기가 등장한다. 이 책의 짝수장을 들여다보면 수학의 역사와 전통적인 분류(산술학, 기하학, 대수학, 해석학)에 대하여 알 수 있다. 저자는 짝수장에 이런 이야기를 배치함으로써 독자들이 지치지 않도록 배려한 것 같다. 로그 적분 함수 Li(N)는 소수 계량 함수 π(N)(N보다 작은 소수의 개수)에 근접한다. 리만 가설을 증명하면 소수 계량 함수를 정확히 파악할 수 있다. 하지만 지금까지 전 세계의 수학자들은 못 풀고 있다. 물론, 수학에서 풀리지 않는 문제들은 많다. 리만 가설은 언제 풀릴지 아무도 장담할 수 없다고 한다. 저자가 일반인을 위해 리만 가설을 설명한 책을 낸 것은 소수 계량 함수 π(N)에 근접하려는 로그 적분 함수 Li(N)라는 생각이 든다.

그래서 300여개의 작은 독일 국가들이 34개의 독립국(오스트리아와 프러시아 포함)과 4개의 자유도시로 통합되었는데 리만은 그 중에 하나인 하노버 왕국의 동쪽인 브레젤렌츠에서 태어났다고 한다. 훔볼트의 개혁으로 수학에서 변방이었던 독일은 두각을 나타낸다. 베를린학술원이 생겼고 리만은 그 혜택을 받은 것 같다. 리만은 괴팅겐대학에 오랫동안 머물면서 연구한다. 괴팅겐대학에는 유명한 수학자인 가우스와 디리클레가 있었다. 리만은 두 수학자를 존경했고 디리클레의 제자였다. 가우스와 디리클레(오일러가 발견한 황금열쇠를 찾아낸)와 리만으로 이어지는 과정에서 리만 가설이 나온 것이다. 리만은 1859년(33세)에 베를린학술원의 회원이 되어 한 편의 논문(주어진 수보다 작은 소수의 개수에 대한 연구)을 냈고 그 논문은 수학의 역사를 바꿔놓았다.

리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | YES24 블로그

선생님이 1부터 100까지 더하는 문제를 냈는데 어린 가우스는 단번에 답을 말했다고 한다. 답은 바로 101*100/2=5050이다. 1부터 100까지 숫자를 한 줄로 늘어트려 놓았을 때, 차례대로 양끝의 숫자 두 개를 더하면 항상 101이다(1…

  • Image source: blog.yes24.com
  • Views: 80051
  • Publish date: 26 minute ago
  • Downloads: 4987
  • Likes: 1711
  • Dislikes: 7
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | Yes24 블로그 - 내 삶의 쉼표
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | Yes24 블로그 – 내 삶의 쉼표

)을 이해하기 위해서는 소수정리를 비롯하여 조화수열, 로그함수, 미적분, 확률, 제타 함수, 복소평면 등의 수학지식을 알고 있어야 한다(알고 있어도 제대로 이해하는 사람은 드물다고 한다). 즉, 진입장벽이 높다. 제타 함수 하나만 해도 정말 특이하고 이해하기 어려운 함수이다. 이 제타 함수를 복소평면에 나타내고 자명하지 않는(허수인) 근들의 실수부가 1/2인 것을 구하는 것만 해도 많은 시간이 걸릴 것이다. 그렇기 때문에 수학에 관심이 있는 사람들만 리만 가설에 도전한다. 이렇게 난해한 리만 가설을 일반인들이 알기 쉽게 책으로 펴냈다는 것은 정말 대단한 것이다. 수학에 대한 전문적인 지식이 없는 일반인들은 이 책 한 권으로 리만 가설을 이해할 수 있다고 나는 말할 수 있다! 저자 더비셔는 리만 가설의 그 높은 진입장벽은 걸어서 넘을 정도로 낮춰줬다. 저자는 아직도 풀리지 않고 있는 리만 가설을 대중들에게 설명하고 혹시나 그 대중들이 관심을 가져서 리만 가설이 풀어지기를 기대한 것은 아닐까?

그 밖에 오일러(러시아의 표트르 대제에게 스카웃당한) 등의 수학자들과 관련된 흥미로운 이야기가 등장한다. 이 책의 짝수장을 들여다보면 수학의 역사와 전통적인 분류(산술학, 기하학, 대수학, 해석학)에 대하여 알 수 있다. 저자는 짝수장에 이런 이야기를 배치함으로써 독자들이 지치지 않도록 배려한 것 같다. 로그 적분 함수 Li(N)는 소수 계량 함수 π(N)(N보다 작은 소수의 개수)에 근접한다. 리만 가설을 증명하면 소수 계량 함수를 정확히 파악할 수 있다. 하지만 지금까지 전 세계의 수학자들은 못 풀고 있다. 물론, 수학에서 풀리지 않는 문제들은 많다. 리만 가설은 언제 풀릴지 아무도 장담할 수 없다고 한다. 저자가 일반인을 위해 리만 가설을 설명한 책을 낸 것은 소수 계량 함수 π(N)에 근접하려는 로그 적분 함수 Li(N)라는 생각이 든다.

그래서 300여개의 작은 독일 국가들이 34개의 독립국(오스트리아와 프러시아 포함)과 4개의 자유도시로 통합되었는데 리만은 그 중에 하나인 하노버 왕국의 동쪽인 브레젤렌츠에서 태어났다고 한다. 훔볼트의 개혁으로 수학에서 변방이었던 독일은 두각을 나타낸다. 베를린학술원이 생겼고 리만은 그 혜택을 받은 것 같다. 리만은 괴팅겐대학에 오랫동안 머물면서 연구한다. 괴팅겐대학에는 유명한 수학자인 가우스와 디리클레가 있었다. 리만은 두 수학자를 존경했고 디리클레의 제자였다. 가우스와 디리클레(오일러가 발견한 황금열쇠를 찾아낸)와 리만으로 이어지는 과정에서 리만 가설이 나온 것이다. 리만은 1859년(33세)에 베를린학술원의 회원이 되어 한 편의 논문(주어진 수보다 작은 소수의 개수에 대한 연구)을 냈고 그 논문은 수학의 역사를 바꿔놓았다.

리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | YES24 블로그

선생님이 1부터 100까지 더하는 문제를 냈는데 어린 가우스는 단번에 답을 말했다고 한다. 답은 바로 101*100/2=5050이다. 1부터 100까지 숫자를 한 줄로 늘어트려 놓았을 때, 차례대로 양끝의 숫자 두 개를 더하면 항상 101이다(1…

  • Image source: blog.yes24.com
  • Views: 32502
  • Publish date: 44 minute ago
  • Downloads: 89320
  • Likes: 4887
  • Dislikes: 2
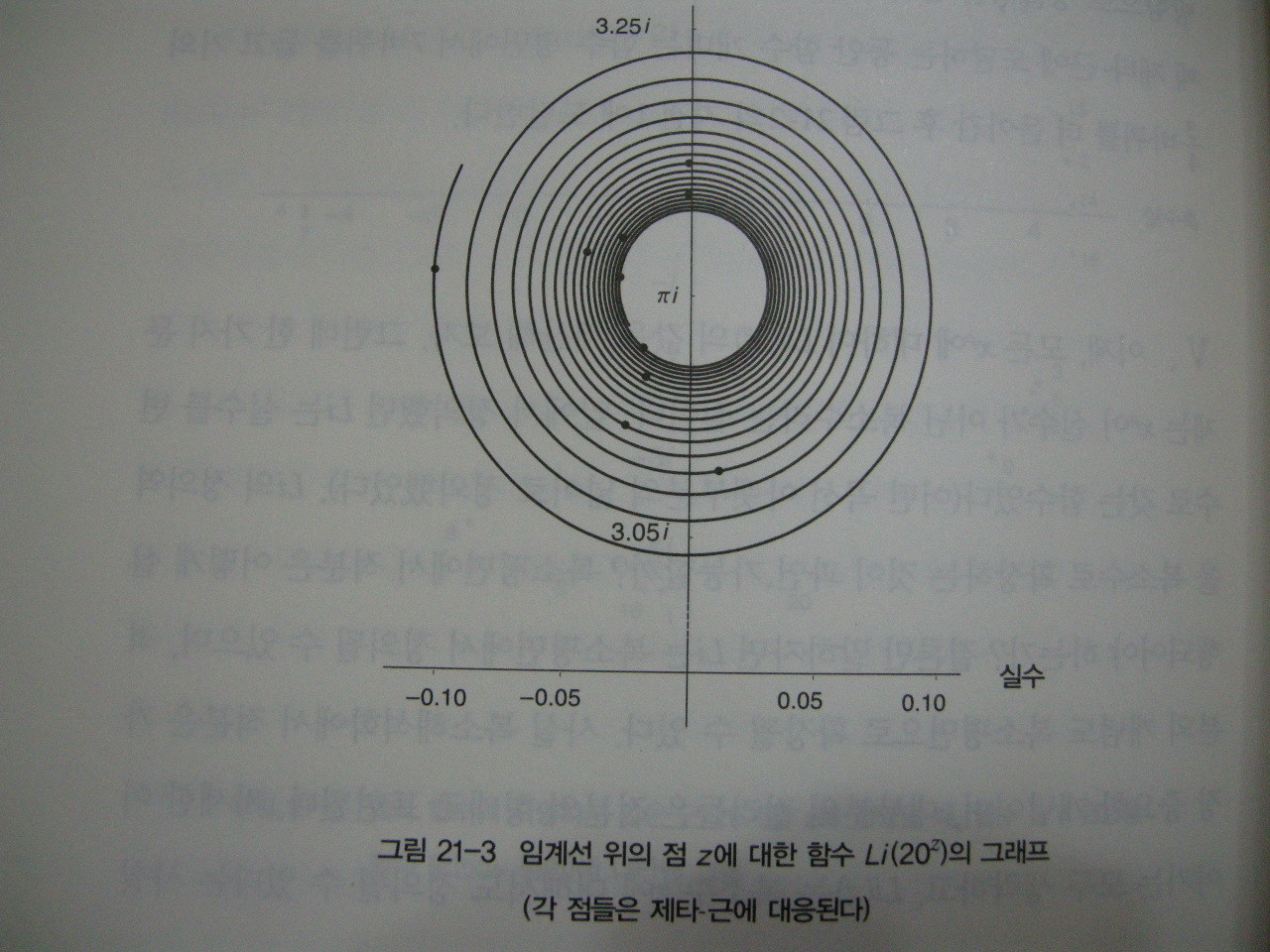
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | Yes24 블로그 - 내 삶의 쉼표
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | Yes24 블로그 – 내 삶의 쉼표

)을 이해하기 위해서는 소수정리를 비롯하여 조화수열, 로그함수, 미적분, 확률, 제타 함수, 복소평면 등의 수학지식을 알고 있어야 한다(알고 있어도 제대로 이해하는 사람은 드물다고 한다). 즉, 진입장벽이 높다. 제타 함수 하나만 해도 정말 특이하고 이해하기 어려운 함수이다. 이 제타 함수를 복소평면에 나타내고 자명하지 않는(허수인) 근들의 실수부가 1/2인 것을 구하는 것만 해도 많은 시간이 걸릴 것이다. 그렇기 때문에 수학에 관심이 있는 사람들만 리만 가설에 도전한다. 이렇게 난해한 리만 가설을 일반인들이 알기 쉽게 책으로 펴냈다는 것은 정말 대단한 것이다. 수학에 대한 전문적인 지식이 없는 일반인들은 이 책 한 권으로 리만 가설을 이해할 수 있다고 나는 말할 수 있다! 저자 더비셔는 리만 가설의 그 높은 진입장벽은 걸어서 넘을 정도로 낮춰줬다. 저자는 아직도 풀리지 않고 있는 리만 가설을 대중들에게 설명하고 혹시나 그 대중들이 관심을 가져서 리만 가설이 풀어지기를 기대한 것은 아닐까?

그 밖에 오일러(러시아의 표트르 대제에게 스카웃당한) 등의 수학자들과 관련된 흥미로운 이야기가 등장한다. 이 책의 짝수장을 들여다보면 수학의 역사와 전통적인 분류(산술학, 기하학, 대수학, 해석학)에 대하여 알 수 있다. 저자는 짝수장에 이런 이야기를 배치함으로써 독자들이 지치지 않도록 배려한 것 같다. 로그 적분 함수 Li(N)는 소수 계량 함수 π(N)(N보다 작은 소수의 개수)에 근접한다. 리만 가설을 증명하면 소수 계량 함수를 정확히 파악할 수 있다. 하지만 지금까지 전 세계의 수학자들은 못 풀고 있다. 물론, 수학에서 풀리지 않는 문제들은 많다. 리만 가설은 언제 풀릴지 아무도 장담할 수 없다고 한다. 저자가 일반인을 위해 리만 가설을 설명한 책을 낸 것은 소수 계량 함수 π(N)에 근접하려는 로그 적분 함수 Li(N)라는 생각이 든다.

그래서 300여개의 작은 독일 국가들이 34개의 독립국(오스트리아와 프러시아 포함)과 4개의 자유도시로 통합되었는데 리만은 그 중에 하나인 하노버 왕국의 동쪽인 브레젤렌츠에서 태어났다고 한다. 훔볼트의 개혁으로 수학에서 변방이었던 독일은 두각을 나타낸다. 베를린학술원이 생겼고 리만은 그 혜택을 받은 것 같다. 리만은 괴팅겐대학에 오랫동안 머물면서 연구한다. 괴팅겐대학에는 유명한 수학자인 가우스와 디리클레가 있었다. 리만은 두 수학자를 존경했고 디리클레의 제자였다. 가우스와 디리클레(오일러가 발견한 황금열쇠를 찾아낸)와 리만으로 이어지는 과정에서 리만 가설이 나온 것이다. 리만은 1859년(33세)에 베를린학술원의 회원이 되어 한 편의 논문(주어진 수보다 작은 소수의 개수에 대한 연구)을 냈고 그 논문은 수학의 역사를 바꿔놓았다.

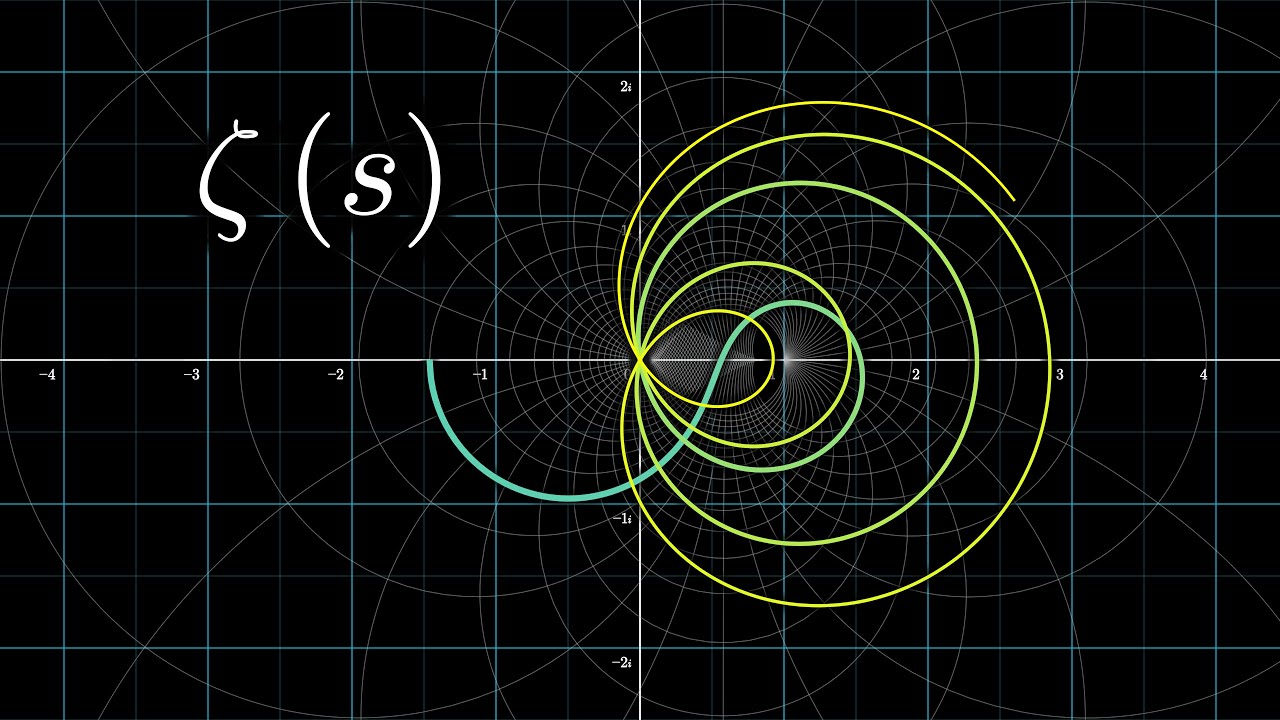
Riemann Hypothesis visualised

  • Image source: ohnym.tistory.com
  • Views: 83865
  • Publish date: 17 hours ago
  • Downloads: 47995
  • Likes: 2557
  • Dislikes: 3
Riemann Hypothesis Visualised
Riemann Hypothesis Visualised

On the Riemann Mapping Theorem ( 리만 사상 정리 )

Riemann Hypothesis visualised

On the Subharmonic function

리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | YES24 블로그

선생님이 1부터 100까지 더하는 문제를 냈는데 어린 가우스는 단번에 답을 말했다고 한다. 답은 바로 101*100/2=5050이다. 1부터 100까지 숫자를 한 줄로 늘어트려 놓았을 때, 차례대로 양끝의 숫자 두 개를 더하면 항상 101이다(1…

  • Image source: blog.yes24.com
  • Views: 64464
  • Publish date: 22 hours ago
  • Downloads: 101170
  • Likes: 8136
  • Dislikes: 8
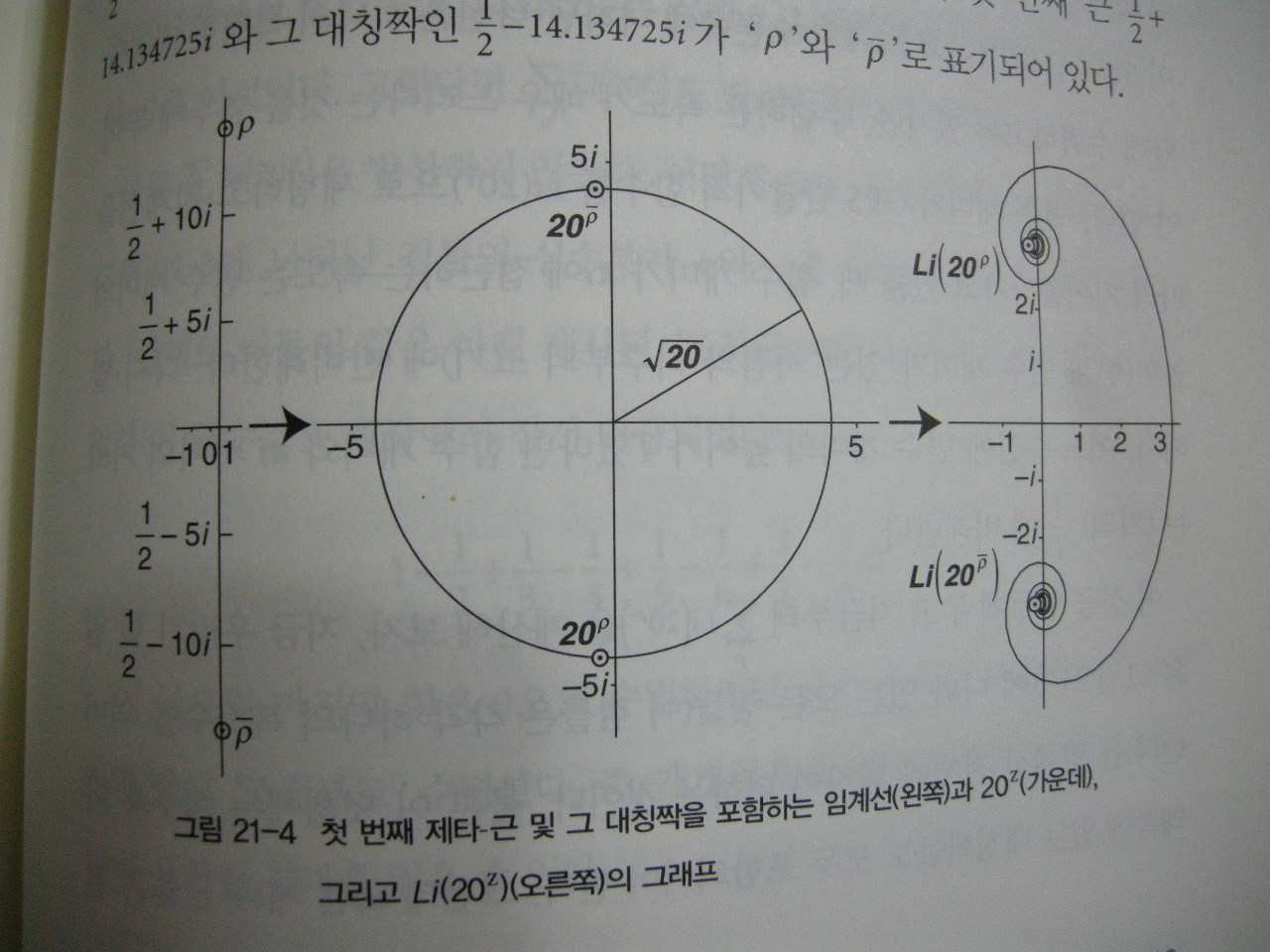
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | Yes24 블로그 - 내 삶의 쉼표
리만 가설 도서 리뷰 : 내가 리만 가설을 어렴풋이 이해하게 되다니! | Yes24 블로그 – 내 삶의 쉼표

)을 이해하기 위해서는 소수정리를 비롯하여 조화수열, 로그함수, 미적분, 확률, 제타 함수, 복소평면 등의 수학지식을 알고 있어야 한다(알고 있어도 제대로 이해하는 사람은 드물다고 한다). 즉, 진입장벽이 높다. 제타 함수 하나만 해도 정말 특이하고 이해하기 어려운 함수이다. 이 제타 함수를 복소평면에 나타내고 자명하지 않는(허수인) 근들의 실수부가 1/2인 것을 구하는 것만 해도 많은 시간이 걸릴 것이다. 그렇기 때문에 수학에 관심이 있는 사람들만 리만 가설에 도전한다. 이렇게 난해한 리만 가설을 일반인들이 알기 쉽게 책으로 펴냈다는 것은 정말 대단한 것이다. 수학에 대한 전문적인 지식이 없는 일반인들은 이 책 한 권으로 리만 가설을 이해할 수 있다고 나는 말할 수 있다! 저자 더비셔는 리만 가설의 그 높은 진입장벽은 걸어서 넘을 정도로 낮춰줬다. 저자는 아직도 풀리지 않고 있는 리만 가설을 대중들에게 설명하고 혹시나 그 대중들이 관심을 가져서 리만 가설이 풀어지기를 기대한 것은 아닐까?

그 밖에 오일러(러시아의 표트르 대제에게 스카웃당한) 등의 수학자들과 관련된 흥미로운 이야기가 등장한다. 이 책의 짝수장을 들여다보면 수학의 역사와 전통적인 분류(산술학, 기하학, 대수학, 해석학)에 대하여 알 수 있다. 저자는 짝수장에 이런 이야기를 배치함으로써 독자들이 지치지 않도록 배려한 것 같다. 로그 적분 함수 Li(N)는 소수 계량 함수 π(N)(N보다 작은 소수의 개수)에 근접한다. 리만 가설을 증명하면 소수 계량 함수를 정확히 파악할 수 있다. 하지만 지금까지 전 세계의 수학자들은 못 풀고 있다. 물론, 수학에서 풀리지 않는 문제들은 많다. 리만 가설은 언제 풀릴지 아무도 장담할 수 없다고 한다. 저자가 일반인을 위해 리만 가설을 설명한 책을 낸 것은 소수 계량 함수 π(N)에 근접하려는 로그 적분 함수 Li(N)라는 생각이 든다.

그래서 300여개의 작은 독일 국가들이 34개의 독립국(오스트리아와 프러시아 포함)과 4개의 자유도시로 통합되었는데 리만은 그 중에 하나인 하노버 왕국의 동쪽인 브레젤렌츠에서 태어났다고 한다. 훔볼트의 개혁으로 수학에서 변방이었던 독일은 두각을 나타낸다. 베를린학술원이 생겼고 리만은 그 혜택을 받은 것 같다. 리만은 괴팅겐대학에 오랫동안 머물면서 연구한다. 괴팅겐대학에는 유명한 수학자인 가우스와 디리클레가 있었다. 리만은 두 수학자를 존경했고 디리클레의 제자였다. 가우스와 디리클레(오일러가 발견한 황금열쇠를 찾아낸)와 리만으로 이어지는 과정에서 리만 가설이 나온 것이다. 리만은 1859년(33세)에 베를린학술원의 회원이 되어 한 편의 논문(주어진 수보다 작은 소수의 개수에 대한 연구)을 냈고 그 논문은 수학의 역사를 바꿔놓았다.

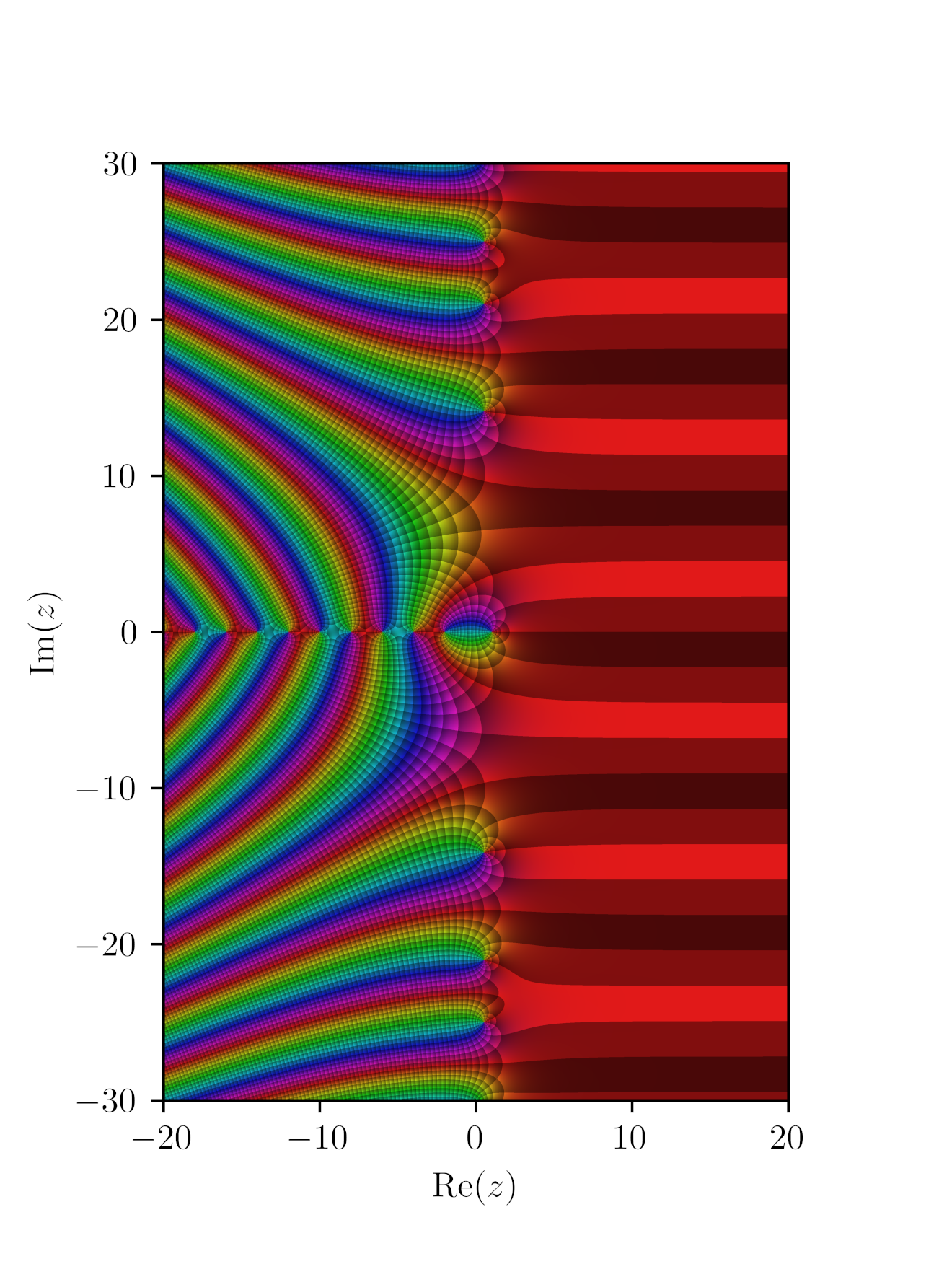
리만 가설 조사하기: Wolfram 언어 12의 신기능

  • Image source: www.wolfram.com
  • Views: 84618
  • Publish date: 28 minute ago
  • Downloads: 92069
  • Likes: 6250
  • Dislikes: 3
리만 가설 조사하기: Wolfram 언어 12의 신기능
리만 가설 조사하기: Wolfram 언어 12의 신기능

이것은 원리상으로는 계산 가능하지만, 아무도 리만 가설을 구축하는 방법을 모르기 때문에 그것에 한정 기호 소거를 적용하면 평가할 수 없게 되어 버립니다(만약 Mathematica가 이 경우에 한정 기호를 풀 수 있다면, 리만 가설의 타당성을 증명할 수 있을 것입니다).

리만 제타 함수의 첫 개의 비자명한 영점은 검정되어 리만 가설을 만족하는 것으로 알려졌 있습니다. 그러므로 이러한 충분한 수치적 증거와 상당한 노력이 이루어지고 있음에도 불구하고 지난 250년 동안 아무도 이 가설을 증명할 수 없었다는 것은 다소 놀랍습니다.

와 깊이 관련된 함수인 함수의 도함수에 의해 주어지는 식의 양수값에 관한 리만 가설의 가장 유명한 대체 문장은 아마도 Li의 부등식일 것입니다. Li의 부등식으로 알려진 이 식은 다음과 같은 공식으로 말할 수 있습니다.

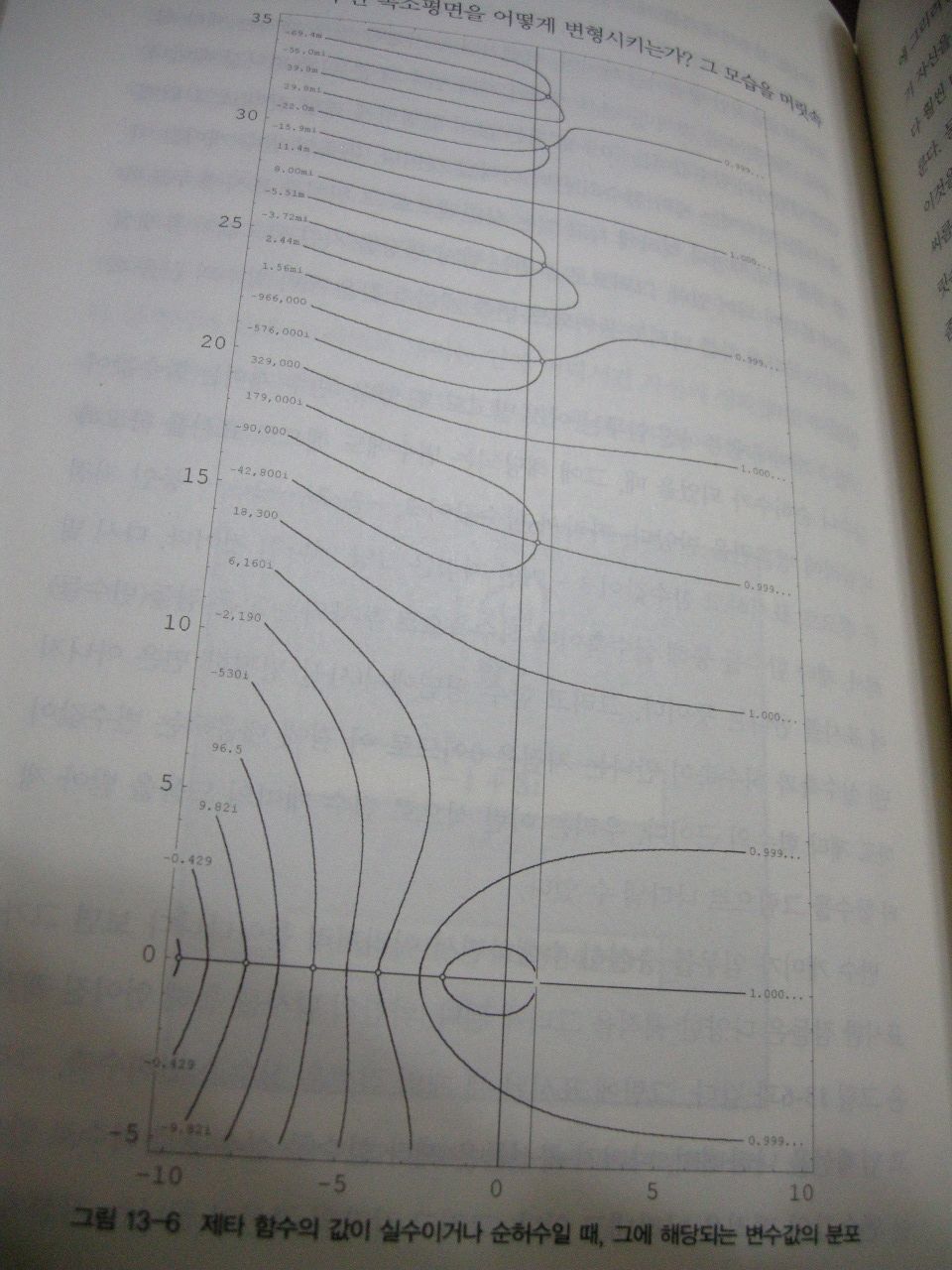
제타 함수란?

제타함수를 처음 연구한 수학자는 오일러(Euler)다. 그 연구를 이어 받아 정의역을 복소수 영역까지 확장하고, 소수(Prime Number)의 연구까지 진행한 인물이 바로 리만(Riemann) 이다. 최고의 수학자들이 무슨 생각을 했는지 한번 알아보자. #제타 함수의 정의 제타함수의 정의는 간단하다. 고등학교에서 배운 무한급수를 다시 보는 것 같다. s에 따라 값이 달라진다. s가 1보다 크거나 값으면 수렴할 것 같은데, 값을 계산하기가 쉽지는 않다. 그래도 계산을 해보자. 아래의 그래프는 s=1일 때의 제타함수(파란색)과 1/x를 1부터 10까지(빨간색) 그린 것이다. 다음의 수식이 성립함을 직관적으로 알 수 있다. 제타함수에서 k = 1 ~ N까지의 부분합과 적분과의 관계이다. 다항식의 적분은 쉽게..

  • Image source: dowhati1.tistory.com
  • Views: 93876
  • Publish date: 12 hours ago
  • Downloads: 35784
  • Likes: 4220
  • Dislikes: 6
제타 함수란?
제타 함수란?

지금까지는 제타함수는 s > 1인 실수 구간에서만 정의가 되었다. 해석적 확장(Analytic Continuation)이라고 불리는 작업을 통해 s = 1 아닌 모든 복소수에 대해서 정의되는 함수로 확장해 보자.

위의 수식(오일러 곱셈 공식, Euler Product Formula)으로 부터 제타함수를 제대로 파악할 수 있으면 소수의 규칙도 알 수 있을 것 같다.

x가 0에 가까이 갈때 sin(x) = x이기 때문에, 극한의 상황을 만족하기 위해서 위 수식을 아래와 같이 변경해 볼 수 있다.

  • Image source: namu.wiki
  • Views: 44690
  • Publish date: 40 minute ago
  • Downloads: 35663
  • Likes: 2185
  • Dislikes: 4
리만 가설 - 나무위키
리만 가설 – 나무위키

실수 함수 PNG 이미지 | PNGWing

  • Image source: www.pngwing.com
  • Views: 8060
  • Publish date: 8 hours ago
  • Downloads: 68368
  • Likes: 5613
  • Dislikes: 8
실수 함수 Png 이미지 | Pngwing
실수 함수 Png 이미지 | Pngwing

실수 함수 PNG 이미지

닮은꼴 함수

  • Image source: namu.moe
  • Views: 91438
  • Publish date: 36 minute ago
  • Downloads: 19769
  • Likes: 3268
  • Dislikes: 5
닮은꼴 함수
닮은꼴 함수

애당초 코사인(cosine)의 이름부터 사인(sine)에 준한다(co-)라는 뜻이다. 그래서 한자로도 사인은 정현(正弦), 코사인은 여현(餘弦)이라고 한다. 90도 위상차를 흔히 여각(餘角)이라고 하기 때문.

[math(\lfloor x \rfloor = -\lceil -x \rceil \Leftrightarrow \lceil x \rceil = -\lfloor -x \rfloor)]

한쪽 함수를 [math(x)]축으로 [math(\pi/2)]만큼 평행이동(shift)하면 완전히 겹치기까지 한다. 즉, 평행이동을 통해 상호 호환이 가능한 함수라는 것이다.

오일러 피 함수 – Wikiwand

수론에서 오일러 파이 함수 function)는 정수환의 몫환의 가역원을 세는 함수이다. 즉, n이 양의 정수일 때, ϕ 은 n과 서로소인 1부터 n까지의 정수의 개수와 같다. 예를 들어, 1부터 6까지의 정수 가운데 1, 5 둘만 6과 서로소이므로, ϕ = 2이다. 1부터 10까지의 정수는 모두 11과 서로소이며, 11은 자기 자신과 서로소가 아니므로, ϕ = 10이다. 1은 자기 자신과 서로소이므로, ϕ = 1이다.

  • Image source: www.wikiwand.com
  • Views: 68553
  • Publish date: 26 minute ago
  • Downloads: 75378
  • Likes: 226
  • Dislikes: 7
오일러 피 함수 - Wikiwand
오일러 피 함수 – Wikiwand

까지의 정수의 개수와 같다. 예를 들어, 1부터 6까지의 정수 가운데 1, 5 둘만 6과 서로소이므로, ϕ(6) = 2이다. 1부터 10까지의 정수는 모두 11과 서로소이며, 11은 자기 자신과 서로소가 아니므로, ϕ(11) = 10이다. 1은 자기 자신과 서로소이므로, ϕ(1) = 1이다.

Euler’s phi (totient) function

오일러 파이 함수

비디오 리만 제타 함수 그래프 전설의 시작 | 바젤 문제 그리고 리만 제타 함수

  • Source: Youtube
  • Views: 67353
  • Date: 16 minute ago
  • Download: 60010
  • Likes: 2798
  • Dislikes: 1

주제에 대한 관련 정보 리만 제타 함수 그래프

Bing에서 리만 제타 함수 그래프 주제에 대한 최신 정보를 볼 수 있습니다.

리만제타함수 계산

리만가설

리만 제타 함수 영점

리만제타함수 해석적확장

리만제타함수 양자역학

리만 제타 함수 자명한 근

리만가설 북한

제타함수 계산기

주제에 대한 기사 보기를 마쳤습니다 리만 제타 함수 그래프. 이 기사가 유용했다면 공유하십시오. 매우 감사합니다.

리만제타함수 계산

리만가설

리만 제타 함수 영점

리만제타함수 해석적확장

리만제타함수 양자역학

리만 제타 함수 자명한 근

리만가설 북한

제타함수 계산기

Leave a Comment